sin x^2は周期関数？

「$\sin x^2$が周期関数でないことを示せ。」

　周期関数の定義は

$$f(x+p)=f(x)\quad(p:定数,p\neq0)$$

が恒等式として成り立つことです。このことと背理法を利用して解きます。

　$\sin x^2$が周期関数であると仮定すると

$$\sin(x+p)^2=\sin x^2$$

が常に成り立つような定数$p$が存在するはずなので、これを満たす$p$を求めます。

移項して

$$\sin(x+p)^2-\sin x^2=0$$

和積の公式より

$$\begin{align*}\sin(x+p)^2-\sin x^2&=2\cos\left\{\frac{(x+p)^2+x^2}{2}\right\}\sin\left\{\frac{(x+p)^2-x^2}{2}\right\}\\[0.5em]&=2\cos\left(\frac{2x^2+2px+p^2}{2}\right)\sin\left(\frac{2px+p^2}{2}\right)\end{align*}$$

なので、

$$\begin{align*}2\cos\left(\frac{2x^2+2px+p^2}{2}\right)\sin\left(\frac{2px+p^2}{2}\right)&=0\\[0.5em]\cos\left(\frac{2x^2+2px+p^2}{2}\right)\sin\left(\frac{2px+p^2}{2}\right)&=0\end{align*}$$

これが成り立つ条件は$\cos\left(\dfrac{2x^2+2px+p^2}{2}\right)=0$または$\sin\left(\dfrac{2px+p^2}{2}\right)=0$となります。

$\cos\left(\dfrac{2x^2+2px+p^2}{2}\right)=0$のとき

$$\begin{align*}\cos\left(\dfrac{2x^2+2px+p^2}{2}\right)&=\cos\left(\frac{2n+1}{2}\pi\right)\quad(n:整数)\\[0.5em]\frac{2x^2+2px+p^2}{2}&=\frac{2n+1}{2}\pi\\[0.5em]2x^2+2px+p^2&=(2n+1)\pi\\[0.5em]2x^2+2px+p^2-(2n+1)\pi&=0\\[0.5em]p^2+2xp+\bigl\{2x^2-(2n+1)\pi\bigr\}&=0\\[0.5em]p&=-x\pm\sqrt{-x^2+(2n+1)\pi}\end{align*}$$

$\sin\left(\dfrac{2px+p^2}{2}\right)=0$のとき

$$\begin{align*}\sin\left(\frac{2px+p^2}{2}\right)&=\sin n\pi\quad(n:整数)\\[0.5em]\frac{2px+p^2}{2}&=n\pi\\[0.5em]2px+p^2&=2n\pi\\[0.5em]2px+p^2-2n\pi&=0\\[0.5em]p^2+2xp-2n\pi&=0\\[0.5em]p&=-x\pm\sqrt{x^2+2n\pi}\end{align*}$$

いずれの場合でも$p$は$x$の関数であり、定数ではありません。
したがって、仮定は誤り、すなわち$\sin x^2$は周期関数でないことがわかります。

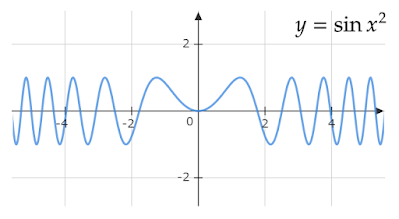
　$y=\sin x^2$のグラフを描いてみると上のようになります。周期関数はx軸方向に周期だけ平行移動すると平行移動前のグラフと全く同じ形になることが特徴ですが、$y=\sin x^2$のグラフはどのように平行移動しても平行移動前のグラフとは同じ形にならないことがわかります。

関連：積和の公式・和積の公式

関連：2次方程式の解の公式と判別式

関連：2次方程式を解く(1)