「次の三角関数の基本周期を求めよ。
(1)$\large\sin2x$
(2)$\large\tan\bigl(-\sqrt{3}x\bigr)$
(3)$\large\cos\left(\dfrac{x}{3}-\dfrac{\pi}{6}\right)$」
三角関数の周期を求めるには、周期関数の定義と基本の三角関数の周期を利用します。
ある関数$f(x)$について$0$でない定数$p$をもちいて
\[f(x+p)=f(x)\]
が常に成り立つとき、$f(x)$は
周期関数といいます。また、このときの$p$のことを
周期といいます。
周期$p$として満足する値のうち、最小の正の数であるもののことを
基本周期といいます。
大抵の場合周期という単語の指すものはこの基本周期のことで、基本周期は
正の周期のうち最小のものというような表現をされる場合もあります。
周期$p$として満足する値はすべてこの基本周期の整数倍となります。
したがって、周期関数において
\[f(x+np)=f(x)\quad(n:整数)\]
もまた常に成り立ちます。
周期関数には三角関数$\sin x,\cos x,\tan x$も含まれます。
整数$n$をもちいると$\sin
x,\cos x$の基本周期は$\mathbf{2\pi}$なので周期は$2n\pi$、$\tan
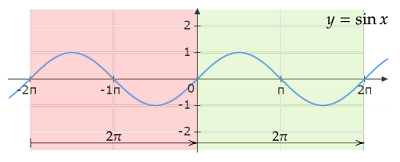
x$の基本周期は$\mathbf{\pi}$なので周期は$n\pi$となります。これらは以下のそれぞれのグラフからも読み取れます。
グラフの色を塗った部分はそれぞれの1周期分の区間を表したものです。周期ごとに同じ値を取り続けているため、各区間のグラフは全く同じ形となります。
以上を踏まえて問題を解きます。
(1)$\sin2x$
$2x=A$とおくと$\sin2x=\sin A$となり、$\sin
A$における基本周期は$2\pi$、周期は$2n\pi$ $(n:整数)$なので
\[\sin(A+2n\pi)=\sin
A\quad(n:整数)\]
が常に成り立ちます。
ここから$A$を$2x$になおし、左辺を変形して$f(x+np)$に相当する形をつくります。
$f(x+np)$は$f(x)$の$x$を$x+np$に変換したものです。なので、変形によって$\sin2(x+np)$という形をつくればよいことになります。このときの$np$から周期がわかります。
\[\sin(2x+2n\pi)=\sin2(x+n\pi)\]
したがって、$\sin2(x+n\pi)=\sin2x$が成り立ち、$f(x+np)=f(x)$の形をつくることができたので、$\sin2x$の周期は$n\pi$であるとわかります。
基本周期は周期のうち最小の正の数なので$n=1$のときの$\mathbf{\pi}$となります。
また、「
関数のグラフを伸び縮みさせる」より$y=\sin2x$のグラフは$y=\sin
x$のグラフのx軸方向の長さを$\dfrac{1}{2}$倍にしたものであるから周期も$2\pi$の$\dfrac{1}{2}$倍の$\pi$である、と求めることもできます。
(2)$\tan\bigl(-\sqrt{3}x\bigr)$
$-\sqrt{3}x=B$とおくと$\tan\bigl(-\sqrt{3}x\bigr)=\tan B$となります。
ここで、$\tan
B$における基本周期は$\pi$、周期は$n\pi$ $(n:整数)$なので
\[\tan(B+n\pi)=\tan
B\]
が常に成り立ちます。
$B$を$-\sqrt{3}x$になおし、左辺を変形して
\begin{align*}\tan\bigl(-\sqrt{3}x+n\pi\bigr)&=\tan\left\{-\sqrt{3}\left(x-\frac{n\pi}{\sqrt{3}}\right)\right\}\\[0.5em]&=\tan\left\{-\sqrt{3}\left(x-\frac{\sqrt{3}\pi
n}{3}\right)\right\}\end{align*}
したがって、$\tan\left\{-\sqrt{3}\left(x-\dfrac{\sqrt{3}\pi
n}{3}\right)\right\}=\tan\bigl(-\sqrt{3}x\bigr)$が成り立つため$\tan\bigl(-\sqrt{3}x\bigr)$の周期は$-\dfrac{\sqrt{3}\pi
n}{3}$であるとわかります。
基本周期は周期のうち最小の正の数なので$n=-1$のときの$\mathbf{\dfrac{\sqrt{3}}{3}\pi}$となります。
また、「
関数のグラフを伸び縮みさせる」と「
関数のグラフの対称移動」より$y=\tan\bigl(-\sqrt{3}x\bigr)$は$y=\tan\Bigl\{-\bigl(\sqrt{3}x\bigr)\Bigr\}$と書くと、$y=\tan
x$のグラフをx軸方向に$\dfrac{1}{\sqrt{3}}$倍した後、y軸に関して対称移動したものであるといえるので、周期は$\pi$の$\dfrac{1}{\sqrt{3}}$倍の$\dfrac{\sqrt{3}}{3}\pi$である、と求めることもできます。
対称移動では周期は変化しません。
(3)$\cos\left(\tfrac{x}{3}-\tfrac{\pi}{6}\right)$
$\dfrac{x}{3}-\dfrac{\pi}{6}=\dfrac{1}{3}x-\dfrac{\pi}{6}=C$とおくと、$\cos\left(\dfrac{x}{3}-\dfrac{\pi}{6}\right)=\cos
C$となり、$\cos C$における基本周期は$2\pi$、周期は$2n\pi$なので
\[\cos(C+2n\pi)=\cos
C\]
が常に成り立ちます。
$C$を$\dfrac{1}{3}x-\dfrac{\pi}{6}$になおして左辺を変形します。
(1)で述べた通り、周期関数の$f(x+np)$とは$f(x)$の$x$を$x+np$に変換したことを意味するので、$f(ax+b)$においては同様の変換後は$f\bigl(a(x+np)+b\bigr)$となります。
したがって、この問題においては$\dfrac{1}{3}x-\dfrac{\pi}{6}$部分の変換後が$\dfrac{1}{3}(x+np)-\dfrac{\pi}{6}$の形になることに注意します。
\begin{align*}\cos\left(\frac{1}{3}x-\frac{\pi}{6}+2n\pi\right)&=\cos\left\{\left(\frac{1}{3}x+2n\pi\right)-\frac{\pi}{6}\right\}\\[0.5em]&=\cos\left\{\frac{1}{3}(x+6n\pi)-\frac{\pi}{6}\right\}\end{align*}
したがって、
\[\cos\left\{\dfrac{1}{3}(x+6n\pi)-\dfrac{\pi}{6}\right\}=\cos\left(\dfrac{1}{3}x-\dfrac{\pi}{6}\right)\]
が成り立つため、$\cos\left(\dfrac{x}{3}-\dfrac{\pi}{6}\right)$の周期は$6n\pi$であることがわかります。
基本周期は周期のうち最小の正の数なので$n=1$のときの$\mathbf{6\pi}$となります。
また、「
関数のグラフを伸び縮みさせる」と「
関数のグラフの平行移動」より$y=\cos\left(\dfrac{x}{3}-\dfrac{\pi}{6}\right)$は$y=\cos
x$のグラフをx軸方向に$3$倍した後、x軸方向に$-\dfrac{\pi}{6}$だけ平行移動したものであるといえるので、周期は$2\pi$の$3$倍の$6\pi$である、と求めることもできます。
平行移動では周期は変化しません。
上の問題は基本の三角関数の周期を利用して基本周期を求めましたが、基本周期を求める公式が存在するので、こちらを利用することで簡単に求められます。
$\sin(ax+b),\cos(ax+b),\tan(ax+b)$ $(a,b:定数)$における周期はそれぞれ
\begin{align*}\sin(ax+b),\cos(ax+b)における周期:&\frac{2\pi}{|a|}\\[1em]\tan(ax+b)における周期:&\frac{\pi}{|a|}\end{align*}
となります。
Share:
https://p-suugaku.blogspot.com/2023/06/sankakukansuu-shuuki.html三角関数の周期を求める
.png)
.png)

.png)
.png)



