相似を利用して円の半径を求める

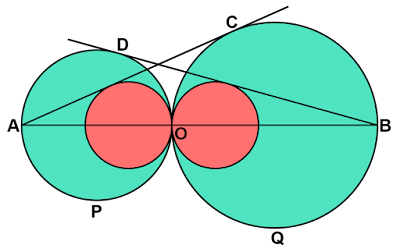
「線分$\text{AB}$を引き、線分$\text{AB}$上の点$\text{A, B}$以外の任意の位置に点$\text{O}$をおく。$\text{AO}$を直径とする円$\text{P}$と$\text{BO}$を直径とする円$\text{Q}$を描く。
点$\text{A}$を通る円$\text{Q}$の接線と、点$\text{B}$を通る円$\text{P}$の接線を引き、それぞれの接点を$\text{C, D}$とする。

このとき、直線$\text{AB}$上に中心があり点$\text{O}$を通る円のうち、直線$\text{AC}$に接する円と直線$\text{BD}$に接する円の半径が等しいことを示せ。」

　これを証明するには、三角形の相似を利用します。

直線$\text{AB}$上に中心があって点$\text{O}$を通る円のうち、直線$\text{AC}$に接する円を$\text{R}$、直線$\text{BD}$に接する円を$\text{S}$とします。円$\text{P, Q, R, S}$の中心もまた$\text{P, Q, R, S}$と呼ぶことにします。

そして、円$\text{R}$と直線$\text{AC}$との接点を$\text{E}$、円$\text{S}$と直線$\text{BD}$との接点を$\text{F}$、円$\text{P, Q, R, S}$の半径をそれぞれ$a,b,r_1,r_2$とします。

　点$\text{Q, R}$からそれぞれ直線$\text{AC}$に垂線をおろします。接線は半径に対し垂直なので垂線はそれぞれ半径である$\text{CQ, ER}$になります。

すると直角三角形$\text{ACQ, AER}$ができます。これらの直角三角形は$∠\text{CAQ}=∠\text{EAR}$なので、直角以外の1組の角が等しいので相似であることがわかります。
また、円の半径を利用してわかる辺の長さを書き出すと$\text{AQ}=2a+b,\text{AR}=2a-r_1,$ $\text{CQ}=b,\text{ER}=r_1$となります。

ここで、相似比より$\text{AQ}:\text{AR}=\text{CQ}:\text{ER}$が成り立つので、それぞれの長さを代入して$r_1$について解くと（ただし、問題の条件より$a>0,b>0$）

\begin{align*}2a+b:2a-r_1&=b:r_1\\[0.5em](2a+b)r_1&=(2a-r_1)b\\[0.5em]\frac{2a+b}{b}r_1&=2a-r_1\\[0.5em]\frac{2a+b}{b}r_1+r_1&=2a\\[0.5em]\frac{2(a+b)}{b}r_1&=2a\\[0.5em]r_1&=\frac{ab}{a+b}\end{align*}

となるので、円$\text{R}$の半径は$\dfrac{ab}{a+b}$であるとわかります。

　点$\text{P, S}$からそれぞれ直線$\text{BD}$に垂線をおろします。

すると直角三角形$\text{BDP, BFS}$ができます。これらの直角三角形は$∠\text{DBP}=∠\text{FBS}$なので、直角以外の1組の角が等しいので相似であることがわかります。
また、円の半径を利用してわかる辺の長さを書き出すと$\text{BP}=a+2b,\text{BS}=2b-r_2,$ $\text{DP}=a,\text{FS}=r_2$となります。

ここで、相似比より$\text{BP}:\text{BS}=\text{DP}:\text{FS}$が成り立つので、それぞれの長さを代入して$r_2$について解くと（前述の通り$a>0,b>0$）

\begin{align*}a+2b:2b-r_2&=a:r_2\\[0.5em](a+2b)r_2&=(2b-r_2)a\\[0.5em]\frac{a+2b}{a}r_2&=2b-r_2\\[0.5em]\frac{2(a+b)}{a}r_2&=2b\\[0.5em]r_2&=\frac{ab}{a+b}\end{align*}

となるので、円$\text{S}$の半径は$\dfrac{ab}{a+b}$であるとわかります。

以上より、円$\text{R}$と円$\text{S}$の半径が等しいことが示されました。

解答例

　直線$\text{AB}$上に中心があり点$\text{O}$を通る円のうち、直線$\text{AC}$に接する円を$\text{R}$、直線$\text{BD}$に接する円$\text{S}$とする。また、円$\text{R}$と直線$\text{AC}$との接点を$\text{E}$、円$\text{S}$と直線$\text{BD}$との接点を$\text{F}$、円$\text{P, Q, R, S}$の半径をそれぞれ$a,b,r_1,r_2$とする。

$△\text{ACQ}$と$△\text{AER}$に着目すると、
$∠\text{ACQ}=∠\text{AER}=90°$、$∠\text{CAQ}=∠\text{EAR}$より2組の角がそれぞれ等しい（または、直角以外の1組の角が等しい）ので相似である。ゆえに$\text{AQ}:\text{AR}=\text{CQ}:\text{ER}$。
$\text{AQ}=2a+b,\text{AR}=2a-r_1,$ $\text{CQ}=b,\text{ER}=r_1$より

\begin{align*}2a+b:2a-r_1&=b:r_1\\[0.5em]r_1&=\frac{ab}{a+b} \tag1\end{align*}

$△\text{BDP}$と$△\text{BFS}$に着目すると、
$∠\text{BDP}=∠\text{BFS}=90°$、$∠\text{DBP}=∠\text{FBS}$より2組の角がそれぞれ等しい（または、直角以外の1組の角が等しい）ので相似である。ゆえに$\text{BP}:\text{BS}=\text{DP}:\text{FS}$。
$\text{BP}=a+2b,\text{BS}=2b-r_2,$ $\text{DP}=a,\text{FS}=r_2$より

\begin{align*}a+2b:2b-r_2&=a:r_2\\[0.5em]r_2&=\frac{ab}{a+b} \tag2\end{align*}

$(1),(2)$より$r_1=r_2$。

したがって、円$\text{R}$と円$\text{S}$の半径は等しい。

リンク