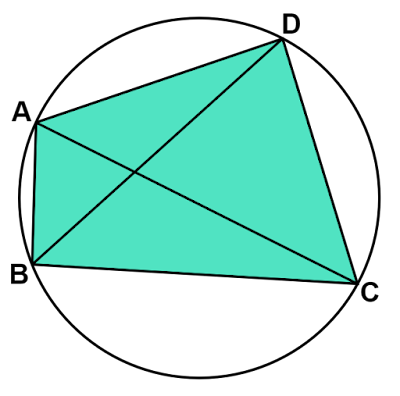
加法定理と正弦定理でトレミーの定理を証明してみる ~ 数学について考えてみる

　トレミーの定理とは、円に内接する四角形

ABCD

$\text{ABCD}$ において

AB \cdot CD + AD \cdot BC = AC \cdot BD

$\large\text{AB}\cdot\text{CD}+\text{AD}\cdot\text{BC}=\text{AC}\cdot\text{BD}$

という関係が成り立つという定理のことです。

これが成り立つことを、加法定理と正弦定理を利用して証明してみます。

　加法定理

sin (x + y) = sin x cos y + cos x sin y

$\sin(x+y)=\sin x\cos y+\cos x\sin y$

の

x, y

$x,y$ にそれぞれ

θ_{1}, θ_{2}

$θ_1,θ_2$ を代入した

\begin{matrix} sin (θ_{1} + θ_{2}) = sin θ_{1} cos θ_{2} + cos θ_{1} sin θ_{2} \\ (1) \end{matrix}

$\begin{equation}\sin(\theta_1+\theta_2)=\sin\theta_1\cos\theta_2+\cos\theta_1\sin\theta_2\end{equation}$

θ_{2}, θ_{3}

$θ_2,θ_3$ を代入した

\begin{matrix} sin (θ_{2} + θ_{3}) = sin θ_{2} cos θ_{3} + cos θ_{2} sin θ_{3} \\ (2) \end{matrix}

$\begin{equation}\sin(\theta_2+\theta_3)=\sin\theta_2\cos\theta_3+\cos\theta_2\sin\theta_3\end{equation}$

をつくり、

(1), (2)

$(1),(2)$ の辺々を掛けます。

\begin{matrix} sin (θ_{1} + θ_{2}) sin (θ_{2} + θ_{3}) = sin θ_{1} sin θ_{2} cos θ_{2} cos θ_{3} + sin θ_{1} {cos}^{2} θ_{2} sin θ_{3} + cos θ_{1} {sin}^{2} θ_{2} cos θ_{3} + cos θ_{1} sin θ_{2} cos θ_{2} sin θ_{3} = sin θ_{1} {cos}^{2} θ_{2} sin θ_{3} + (sin θ_{1} cos θ_{3} + cos θ_{1} sin θ_{3}) sin θ_{2} cos θ_{2} + cos θ_{1} {sin}^{2} θ_{2} cos θ_{3} = sin θ_{1} {cos}^{2} θ_{2} sin θ_{3} + sin (θ_{1} + θ_{3}) sin θ_{2} cos θ_{2} + cos θ_{1} {sin}^{2} θ_{2} cos θ_{3} \end{matrix}

$\begin{align*}&\sin(\theta_1+\theta_2)\sin(\theta_2+\theta_3)\\ &\quad=\sin\theta_1\sin\theta_2\cos\theta_2\cos\theta_3+\sin\theta_1\cos^2\theta_2\sin\theta_3\\ &\qquad+\cos\theta_1\sin^2\theta_2\cos\theta_3+\cos\theta_1\sin\theta_2\cos\theta_2\sin\theta_3\\[0.5em]&\quad=\sin\theta_1\cos^2\theta_2\sin\theta_3\\ &\qquad+(\sin\theta_1\cos\theta_3+\cos\theta_1\sin\theta_3)\sin\theta_2\cos\theta_2\\ &\qquad+\cos\theta_1\sin^2\theta_2\cos\theta_3\\[0.5em]&\quad=\sin\theta_1\cos^2\theta_2\sin\theta_3\\ &\qquad+\sin(\theta_1+\theta_3)\sin\theta_2\cos\theta_2+\cos\theta_1\sin^2\theta_2\cos\theta_3\end{align*}$

三角関数の相互関係

{sin}^{2} x + {cos}^{2} x = 1

$\sin^2x+\cos^2x=1$ より

{cos}^{2} x = 1 - {sin}^{2} x

$\cos^2x=1-\sin^2x$ なので

\begin{matrix} sin (θ_{1} + θ_{2}) sin (θ_{2} + θ_{3}) = sin θ_{1} (1 - {sin}^{2} θ_{2}) sin θ_{3} + sin (θ_{1} + θ_{3}) sin θ_{2} cos θ_{2} + cos θ_{1} {sin}^{2} θ_{2} cos θ_{3} = sin θ_{1} sin θ_{3} + sin (θ_{1} + θ_{3}) sin θ_{2} cos θ_{2} + (cos θ_{1} cos θ_{3} - sin θ_{1} sin θ_{3}) {sin}^{2} θ_{2} \end{matrix}

$\begin{align*}&\sin(\theta_1+\theta_2)\sin(\theta_2+\theta_3)\\ &\quad=\sin\theta_1(1-\sin^2\theta_2)\sin\theta_3+\sin(\theta_1+\theta_3)\sin\theta_2\cos\theta_2\\ &\qquad+\cos\theta_1\sin^2\theta_2\cos\theta_3\\[0.5em]&\quad=\sin\theta_1\sin\theta_3+\sin(\theta_1+\theta_3)\sin\theta_2\cos\theta_2\\ &\qquad+(\cos\theta_1\cos\theta_3-\sin\theta_1\sin\theta_3)\sin^2\theta_2\end{align*}$

加法定理

cos (x + y) = cos x cos y - sin x sin y

$\cos(x+y)=\cos x\cos y-\sin x\sin y$ より

\begin{matrix} sin (θ_{1} + θ_{2}) sin (θ_{2} + θ_{3}) = sin θ_{1} sin θ_{3} + sin (θ_{1} + θ_{3}) sin θ_{2} cos θ_{2} + cos (θ_{1} + θ_{3}) {sin}^{2} θ_{2} = sin θ_{1} sin θ_{3} + sin θ_{2} {sin (θ_{1} + θ_{3}) cos θ_{2} + cos (θ_{1} + θ_{3}) sin θ_{2}} = sin θ_{1} sin θ_{3} + sin θ_{2} sin (θ_{1} + θ_{2} + θ_{3}) \end{matrix}

$\begin{align*}&\sin(\theta_1+\theta_2)\sin(\theta_2+\theta_3)\\ &\quad=\sin\theta_1\sin\theta_3\\ &\qquad+\sin(\theta_1+\theta_3)\sin\theta_2\cos\theta_2+\cos(\theta_1+\theta_3)\sin^2\theta_2\\[0.5em]&\quad=\sin\theta_1\sin\theta_3\\ &\qquad+\sin\theta_2\bigl\{\sin(\theta_1+\theta_3)\cos\theta_2+\cos(\theta_1+\theta_3)\sin\theta_2\bigr\}\\[0.5em]&\quad=\sin\theta_1\sin\theta_3+\sin\theta_2\sin(\theta_1+\theta_2+\theta_3)\end{align*}$

180 ° - (θ_{1} + θ_{2} + θ_{3}) = θ_{4}

$180°-(θ_1+θ_2+θ_3)=θ_4$ とすると、三角関数の性質

sin (180 ° - x) = sin x

$\sin(180°-x)=\sin x$ より

\begin{matrix} sin (θ_{1} + θ_{2}) sin (θ_{2} + θ_{3}) & = sin θ_{1} sin θ_{3} + sin θ_{2} sin θ_{4} (た だ し 、 t h e t a_{1} + θ_{2} + θ_{3} + θ_{4} = 180 °) \end{matrix}

$\begin{align*}\sin(\theta_1+\theta_2)\sin(\theta_2+\theta_3)&=\sin\theta_1\sin\theta_3+\sin\theta_2\sin\theta_4\\ &(ただし、theta_1+\theta_2+\theta_3+\theta_4=180°)\end{align*}$

が成り立つことがわかります。

さらに両辺に

4 R^{2}

$4R^2$

(R > 0)

$(R>0)$ を掛けて

\begin{matrix} \begin{matrix} 4 R^{2} sin (θ_{1} + θ_{2}) sin (θ_{2} + θ_{3}) = 4 R^{2} sin θ_{1} sin θ_{3} + 4 R^{2} sin θ_{2} sin θ_{4} \end{matrix} \\ (3) \end{matrix}

$\begin{equation}\begin{aligned}&4R^2\sin(\theta_1+\theta_2)\sin(\theta_2+\theta_3)\\ &\quad=4R^2\sin\theta_1\sin\theta_3+4R^2\sin\theta_2\sin\theta_4\end{aligned}\end{equation}$

とします。

　話は変わって半径

R

$R$ の円に内接する四角形

ABCD

$\text{ABCD}$ について考えます。

弦

AB

$\text{AB}$ に対する円周角

∠ ACB, ∠ ADB

$∠\text{ACB},∠\text{ADB}$ の大きさを

θ_{1}

$θ_1$ 、弦

BC

$\text{BC}$ に対する円周角

∠ BAC, ∠ BDC

$∠\text{BAC},∠\text{BDC}$ の大きさを

θ_{2}

$θ_2$ 、弦

CD

$\text{CD}$ に対する円周角

∠ CAD, ∠ CBD

$∠\text{CAD},∠\text{CBD}$ の大きさを

θ_{3}

$θ_3$ 、弦

AD

$\text{AD}$ に対する円周角

∠ ABD, ∠ ACD

$∠\text{ABD},∠\text{ACD}$ の大きさを

θ_{4}

$θ_4$ とします。

このとき円に内接する四角形の性質より

\begin{matrix} ∠ ADC + ∠ ABC & = (θ_{1} + θ_{2}) + (θ_{3} + θ_{4}) = 180 ° ∴ θ_{1} + θ_{2} + θ_{3} + θ_{4} & = 180 ° \end{matrix}

$\begin{align*}∠\text{ADC}+∠\text{ABC}&=(\theta_1+\theta_2)+(\theta_3+\theta_4)\\[0.5em]&=180°\\[0.5em]\therefore\theta_1+\theta_2+\theta_3+\theta_4&=180°\end{align*}$

が成り立ちます。（つまり、

(3)

$(3)$ における角度の条件を満たしています。）

また、

△ ACD

$△\text{ACD}$ に着目して正弦定理より

\frac{AC}{sin (θ_{1} + θ_{2})} = \frac{CD}{sin θ_{3}} = \frac{AD}{sin θ_{4}} = 2 R

$\frac{\text{AC}}{\sin(\theta_1+\theta_2)}=\frac{\text{CD}}{\sin\theta_3}=\frac{\text{AD}}{\sin\theta_4}=2R$

であることから

\begin{matrix} AC & = 2 R sin (θ_{1} + θ_{2}) CD & = 2 R sin θ_{3} AD & = 2 R sin θ_{4} \\ (4) (5) (6) \end{matrix}

$\begin{align}\text{AC}&=2R\sin(\theta_1+\theta_2)\\[1em]\text{CD}&=2R\sin\theta_3\\[1em]\text{AD}&=2R\sin\theta_4\end{align}$

が成り立ちます。

同様に

△ ABD

$△\text{ABD}$ に着目して

\frac{BD}{sin (θ_{2} + θ_{3})} = \frac{AB}{sin θ_{1}} = 2 R

$\frac{\text{BD}}{\sin(\theta_2+\theta_3)}=\frac{\text{AB}}{\sin\theta_1}=2R$

であることから

\begin{matrix} BD & = 2 R sin (θ_{2} + θ_{3}) AB & = 2 R sin θ_{1} \\ (7) (8) \end{matrix}

$\begin{align}\text{BD}&=2R\sin(\theta_2+\theta_3)\\[1em]\text{AB}&=2R\sin\theta_1\end{align}$

が、

△ ABC

$△\text{ABC}$ に着目して

\frac{BC}{sin θ_{2}} = 2 R

$\frac{\text{BC}}{\sin\theta_2}=2R$

であることから

\begin{matrix} BC = 2 R sin θ_{2} \\ (9) \end{matrix}

$\begin{equation}\text{BC}=2R\sin\theta_2\end{equation}$

が成り立ちます。

ここで、

(3)

$(3)$ を変形して

(4) ～ (9)

$(4)～(9)$ を代入すると

$\begin{align*}&2R\sin(\theta_1+\theta_2)\cdot2R\sin(\theta_2+\theta_3)\\ &\quad=2R\sin\theta_1\cdot2R\sin\theta_3+2R\sin\theta_2\cdot2R\sin\theta_4\\[0.5em]&\text{AC}\cdot \text{BD}=\text{AB}\cdot\text{CD}+\text{BC}\cdot\text{AD}\end{align*}$

すなわち、

$\text{AB}\cdot\text{CD}+\text{AD}\cdot\text{BC}=\text{AC}\cdot\text{BD}$

となるため、トレミーの定理は成り立つことがわかります。