鈍角三角形の3本の垂線の性質

　鋭角三角形の各頂点から対辺におろした3本の垂線にはどのような性質があるでしょうか？

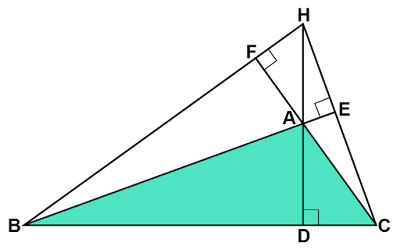
角度に関する性質

　3本の垂線の交点である垂心$\text{H}$周りにできる角の大きさを調べます。

　$△\text{AEH}$と$△\text{ADB}$に着目すると、$∠\text{AEH}=∠\text{ADB}=90°$、対頂角$∠\text{EAH}=∠\text{DAB}$より、2組の角がそれぞれ等しいので相似であることがわかります。

このことから$∠\text{AHE}=∠\text{B}$です。

　$△\text{AFH}$と$△\text{ADC}$に着目すると、$∠\text{AFH}=∠\text{ADC}=90°$、対頂角$∠\text{FAH}=∠\text{DAC}$より、2組の角がそれぞれ等しいので相似であることがわかります。

このことから$∠\text{AHF}=∠\text{C}$です。

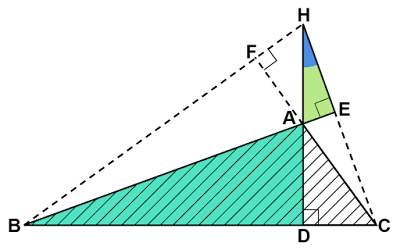
垂心周りの他の4つの角のうち2つは$∠\text{AEH, }∠\text{AFH}$の対頂角で、残る2つの角は$∠\text{BHC}$の外角となります。
$∠\text{BHC}=∠\text{B}+∠\text{C}$で隣り合う内角と外角の和は$180°$であることから、外角の大きさは$∠\text{A}$に等しいことがわかります。

したがって、鈍角三角形の垂心周りの角は鋭角三角形のときと同様、その三角形の内角と等しい大きさの角が集まっていることがわかります。

関連：鋭角三角形の3本の垂線の性質

長さに関する性質

　3本の垂線の長さや垂線や垂心によって分割されてできる線分の長さを調べます。

　$△\text{ABD}$に着目すると

$$\text{BD}=\text{AB}\cos∠\text{B}$$

$△\text{ACD}$に着目すると

$$\text{CD}=\text{AC}\cos∠\text{C}$$

両方の三角形より

$$\text{AD}=\text{AB}\sin∠\text{B}=\text{AC}\sin∠\text{C}$$

であることがわかります。

関連：三角関数の読み方　①三角比の読み方

ここで、正弦定理より

$$\begin{align*}\frac{\text{BC}}{\sin∠\text{A}}=\frac{\text{AC}}{\sin∠\text{B}}=\frac{\text{AB}}{\sin∠\text{C}}&=2R\\ &(R:外接円の半径)\end{align*}$$

であり、これを変形すると

$$\begin{align}\text{BC}&=2R\sin∠\text{A}\\[1em]\text{AC}&=2R\sin∠\text{B}\\[1em]\text{AB}&=2R\sin∠\text{C}\end{align}$$

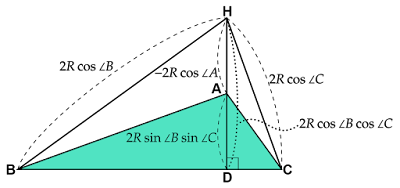
が得られます。これらを利用して各線分の長さを表すと

$$\begin{align*}\text{BD}&=2R\cos∠\text{B}\sin∠\text{C}\\[1em]\text{CD}&=2R\sin∠\text{B}\cos∠\text{C}\\[1em]\text{AD}&=2R\sin∠\text{B}\sin∠\text{C}\end{align*}$$

となります。

関連：正弦定理

　$△\text{BDH}$に着目すると

$$\text{BH}=\frac{\text{BD}}{\sin∠\text{BHD}}$$

$△\text{CDH}$に着目すると

$$\text{CH}=\frac{\text{CD}}{\sin∠\text{CHD}}$$

両方の三角形より

$$\text{DH}=\text{BH}\cos∠\text{BHD}=\text{CH}\cos∠\text{CHD}$$

となります。

上で$\text{BD}=2R\cos∠\text{B}\sin∠\text{C, CD}=2R\sin∠\text{B}\cos∠\text{C, }$$∠\text{BHD}=∠\text{C, }∠\text{CHD}=∠\text{B}$であることがわかったので、これらを代入すると

$$\begin{align*}\text{BH}&=2R\cos∠\text{B}\\[1em]\text{CH}&=2R\cos∠\text{C}\\[1em]\text{DH}&=2R\cos∠\text{B}\cos∠\text{C}\end{align*}$$

となります。

　$△\text{BCF}$に着目すると

$$\text{BF}=\text{BC}\sin∠\text{C}$$

$△\text{CFH}$に着目すると

$$\text{FH}=\text{CH}\cos∠\text{CHF}$$

両方の三角形より

$$\text{CF}=\text{BC}\cos∠\text{C}=\text{CH}\sin∠\text{CHF}$$

となります。

$(1)$、$\text{CH}=2R\cos∠\text{C}$、$∠\text{CHF}=∠\text{B}+∠\text{C}=180°-∠\text{A}$を利用すると

$$\begin{align*}\text{BF}&=2R\sin∠\text{A}\sin∠\text{C}\\[1em]\text{FH}&=2R\cos∠\text{C}\cos(180°-∠\text{A})\\[0.5em]&=-2R\cos∠\text{A}\cos∠\text{C}&\bigl(\because \cos(180°-\theta)=-\cos\theta\bigr)\\[1em]\text{CF}&=2R\sin∠\text{A}\cos∠\text{C}\end{align*}$$

となります。線分$\text{FH}$の長さにマイナスが付くのは$∠\text{A}$が鈍角で$\cos∠\text{A}$が負の値となるためです。

　$△\text{BCE}$に着目すると

$$\text{CE}=\text{BC}\sin∠\text{B}$$

$△\text{BEH}$に着目すると

$$\text{EH}=\text{BH}\cos∠\text{BHE}$$

両方の三角形より

$$\text{BE}=\text{BC}\cos∠\text{B}=\text{BH}\sin∠\text{BHE}$$

となります。

$(1)$、$\text{BH}=2R\cos∠\text{B}$、$∠\text{BHE}=180°-∠\text{A}$を利用すると

$$\begin{align*}\text{CE}&=2R\sin∠\text{A}\sin∠\text{B}\\[1em]\text{EH}&=2R\cos∠\text{B}\cos(180°-∠\text{A})\\[0.5em]&=-2R\cos∠\text{A}\cos∠\text{B}\\[1em]\text{BE}&=2R\sin∠\text{A}\cos∠\text{B}\end{align*}$$

となります。

　$△\text{AEH}$に着目すると

$$\text{AE}=\text{EH}\tan∠\text{AHE}$$

$△\text{AFH}$に着目すると

$$\text{AF}=\text{FH}\tan∠\text{AHF}$$

両方の三角形より

$$\text{AH}=\frac{\text{EH}}{\cos∠\text{AHE}}=\frac{\text{FH}}{\cos∠\text{AHF}}$$

となります。

上で$\text{EH}=-2R\cos∠\text{A}\cos∠\text{B, FH}=-2R\cos∠\text{A}\cos∠\text{C}$、$∠\text{AHE}=∠\text{B, }∠\text{AHF}=∠\text{C}$であることがわかったので、これらを代入すると

$$\begin{align*}\text{AE}&=-2R\cos∠\text{A}\cos∠\text{B}\tan∠\text{B}\\[0.5em]&=-2R\cos∠\text{A}\cos∠\text{B}\cdot\frac{\sin∠\text{B}}{\cos∠\text{B}}\\[0.5em]&=-2R\cos∠\text{A}\sin∠\text{B}\\[1em]\text{AF}&=-2R\cos∠\text{A}\cos∠\text{C}\tan∠\text{C}\\[0.5em]&=-2R\cos∠\text{A}\sin∠\text{C}\\[1em]\text{AH}&=-2R\cos∠\text{A}\end{align*}$$

となります。

垂心$\text{H}$と各頂点を通る直線を引いたときにできる線分の長さは以下のようになります。

相似に関する性質

　垂心$\text{H}$を頂点の1つとする直角三角形の相似について調べます。

　$△\text{HBD}$と$△\text{HAF}$に着目すると、$∠\text{HDB}=∠\text{HFA}=90°$と共通の角$∠\text{BHD}=∠\text{AHF}$より2組の角がそれぞれ等しいので相似であることがわかります。

また、その相似比は$\text{BD}=2R\cos∠\text{B}\sin∠\text{C, AF}=-2R\cos∠\text{A}\sin∠\text{C}$より$\text{BD}:\text{AF}=\cos∠\text{B}:-\cos∠\text{A}$となります。

　$△\text{HCD}$と$△\text{HAE}$に着目すると、$∠\text{HDC}=∠\text{HEA}=90°$、共通の角$∠\text{CHD}=∠\text{AHE}$より2組の角がそれぞれ等しいので相似であることがわかります。

また、その相似比は$\text{CD}=2R\sin∠\text{B}\cos∠\text{C, AE}=-2R\cos∠\text{A}\sin∠\text{B}$より$\text{CD}:\text{AE}=\cos∠\text{C}:-\cos∠\text{A}$となります。

　$△\text{HBE}$と$△\text{HCF}$に着目すると、$∠\text{BEH}=∠\text{CFH}=90°$、共通の角$∠\text{BHE}=∠\text{CHF}$より2組の角がそれぞれ等しいので相似であることがわかります。

また、その相似比は$\text{BH}=2R\cos∠\text{B, CH}=2R\cos∠\text{C}$より$\text{BH}:\text{CH}=\cos∠\text{B}:\cos∠\text{C}$となります。

関連：鋭角三角形の3本の垂線の性質

関連：直角三角形の垂線の性質