鋭角三角形の3本の垂線の性質

　鋭角三角形の各頂点から対辺におろした3本の垂線にはどのような性質があるでしょうか？

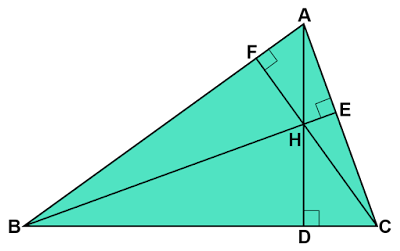
角度に関する性質

　3本の垂線の交点である垂心の周りにできる6つの角。これらの大きさを調べます。

　四角形$\text{AEHF}$に着目すると、$∠\text{AEH}=∠\text{AFH}=90°$より対角の和が$180°$なので、この四角形は円に内接します。

円に内接する四角形の性質より、内角とその対角に隣り合う外角の大きさは等しくなるので

$$∠\text{A}=∠\text{BHF}=∠\text{CHE}$$

が成り立ちます。

関連：円に内接する四角形の対角の和はなぜ$180°$なのか？

　同様にして四角形$\text{BDHF}$に着目すれば

$$∠\text{B}=∠\text{AHF}=∠\text{CHD}$$

が、四角形$\text{CDHE}$に着目すれば

$$∠\text{C}=∠\text{AHE}=∠\text{BHD}$$

が導かれます。

したがって、垂心周りの6つの角はすべてその三角形の内角の大きさを持つことがわかります。

長さに関する性質

　垂線の長さと垂線や垂心によって分割されてできる線分の長さを調べます。

　$△\text{ABD}$に着目すると

$$\text{BD}=\text{AB}\cos∠\text{B}$$

$△\text{ACD}$に着目すると

$$\text{CD}=\text{AC}\cos∠\text{C}$$

であることがわかります。

また、垂線$\text{AD}$の長さは

$$\text{AD}=\text{AB}\sin∠\text{B}=\text{AC}\sin∠\text{C}$$

であることがわかります。

関連：三角関数の読み方　①三角比の読み方

ここで、正弦定理より

$$\begin{align*}\frac{\text{BC}}{\sin∠\text{A}}=\frac{\text{AC}}{\sin∠\text{B}}=\frac{\text{AB}}{\sin∠\text{C}}&=2R\\ &(R:外接円の半径)\end{align*}$$

であり、これを変形すると

$$\begin{align}\text{BC}&=2R\sin∠\text{A}\\[1em]\text{AC}&=2R\sin∠\text{B}\\[1em]\text{AB}&=2R\sin∠\text{C}\end{align}$$

が得られます。これらを利用して各線分の長さを表すと

$$\begin{align*}\text{BD}&=2R\cos∠\text{B}\sin∠\text{C}\\[1em]\text{CD}&=2R\sin∠\text{B}\cos∠\text{C}\\[1em]\text{AD}&=2R\sin∠\text{B}\sin∠\text{C}\end{align*}$$

となります。

関連：正弦定理

　$△\text{ABE}$に着目すると

$$\text{AE}=\text{AB}\cos∠\text{A}$$

$△\text{BCE}$に着目すると

$$\text{CE}=\text{BC}\cos∠\text{C}$$

であることがわかります。

また、垂線$\text{BE}$の長さは

$$\text{BE}=\text{AB}\sin∠\text{A}=\text{BC}\sin∠\text{C}$$

となります。

これらに対し正弦定理を利用して得られた$(1), (3)$を利用すれば

$$\begin{align*}\text{AE}&=2R\cos∠\text{A}\sin∠\text{C}\\[1em]\text{CE}&=2R\sin∠\text{A}\cos∠\text{C}\\[1em]\text{BE}&=2R\sin∠\text{A}\sin∠\text{C}\end{align*}$$

となります。

　$△\text{BCF}$に着目すると

$$\text{BF}=\text{BC}\cos∠\text{B}$$

$△\text{ACF}$に着目すると

$$\text{AF}=\text{AC}\cos∠\text{A}$$

であることがわかります。

また、垂線$\text{CF}$の長さは

$$\text{CF}=\text{BC}\sin∠\text{B}=\text{AC}\sin∠\text{A}$$

となります。

これらに対し$(1), (2)$を利用すれば

$$\begin{align*}\text{BF}&=2R\sin∠\text{A}\cos∠\text{B}\\[1em]\text{AF}&=2R\cos∠\text{A}\sin∠\text{B}\\[1em]\text{CF}&=2R\sin∠\text{A}\sin∠\text{B}\end{align*}$$

となります。

　次に、各垂線を垂心で分割してできる線分の長さを調べてみます。

　$△\text{AEH}$に着目すると$\text{AH}=\dfrac{\text{AE}}{\sin∠\text{AHE}}, \text{EH}=\text{AH}\cos∠\text{AHE}$です。

上で$\text{AE}=2R\cos∠\text{A}\sin∠\text{C, }∠\text{AHE}=∠\text{C}$であることがわかったので、これらを代入すると

$$\begin{align*}\text{AH}&=\frac{2R\cos∠\text{A}\sin∠\text{C}}{\sin∠\text{C}}\\[0.5em]&=2R\cos∠\text{A}\\[1em]\text{EH}&=2R\cos∠\text{A}\cos∠\text{C}\end{align*}$$

となることがわかります。

　$△\text{BEH}$に着目すると$\text{BH}=\dfrac{\text{BF}}{\sin∠\text{BHF}}, \text{FH}=\text{BH}\cos∠\text{BHF}$です。

上で$\text{BF}=2R\sin∠\text{A}\cos∠\text{B, }∠\text{BHF}=∠\text{A}$であることがわかったので、これらを代入すると

$$\text{BH}=2R\cos∠\text{B, FH}=2R\cos∠\text{A}\cos∠\text{B}$$

となることがわかります。

　$△\text{CDH}$に着目すると$\text{CH}=\dfrac{\text{CD}}{\sin∠\text{CHD}}, \text{DH}=\text{CH}\cos∠\text{CHD}$です。

上で$\text{CD}=2R\sin∠\text{B}\cos∠\text{C, }∠\text{CHD}=∠\text{B}$であることがわかったので、これらを代入すると

$$\text{CH}=2R\cos∠\text{C, DH}=2R\cos∠\text{B}\cos∠\text{C}$$

となることがわかります。

　$△\text{ABC}$に垂線$\text{AD}$と垂心$\text{H}$を描き加えたときの各線分の長さは以下のようになります。3辺の長さを利用すると1つの線分の長さを表す式が複数出てきますが、外接円の半径を利用することで1つの式で表すことができるようになります。

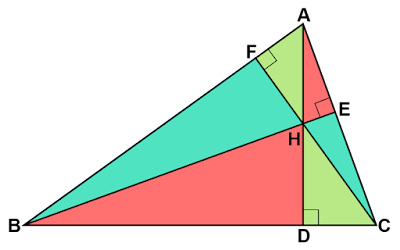
合同・相似に関する性質

　垂心を頂点の1つとする6つの直角三角形の間にある関係について調べます。

　$△\text{BFH}$と$△\text{CEH}$に着目すると、$∠\text{BFH}=∠\text{CEH}=90°$、$∠\text{BHF}=∠\text{CHE}=∠\text{A}$より、2組の角がそれぞれ等しいので相似であることがわかります。

また、その相似比は$\text{BH}=2R\cos∠\text{B, CH}=2R\cos∠\text{C}$より$\text{BH}:\text{CH}=\cos∠\text{B}:\cos∠\text{C}$となります。

　$△\text{AFH}$と$△\text{CDH}$に着目すると、$∠\text{AFH}=∠\text{CDH}=90°$、$∠\text{AHF}=∠\text{CHD}=∠\text{B}$より、2組の角がそれぞれ等しいので相似であることがわかります。

また、その相似比は$\text{AH}=2R\cos∠\text{A, CH}=2R\cos∠\text{C}$より$\text{AH}:\text{CH}=\cos∠\text{A}:\cos∠\text{C}$となります。

　$△\text{AEH}$と$△\text{BDH}$に着目すると、$∠\text{AEH}=∠\text{BDH}=90°$、$∠\text{AHE}=∠\text{BHD}=∠\text{C}$より、2組の角がそれぞれ等しいので相似であることがわかります。

また、その相似比は$\text{AH}=2R\cos∠\text{A, BH}=2R\cos∠\text{B}$より$\text{AH}:\text{BH}=\cos∠\text{A}:\cos∠\text{B}$となります。

したがって、垂心周りの角で対頂角の関係にある角を内角に持つ直角三角形は相似の関係にあることがわかります。

三角形$\text{ABC}$が二等辺三角形の場合、底辺の垂直二等分線に関して対称な位置関係にある直角三角形は合同となります。

また、正三角形の場合には6つの直角三角形全てが合同となります。

関連：直角三角形の垂線の性質

関連：鈍角三角形の3本の垂線の性質