10は3の倍数ではないので、これまでに求めた角度における三角比を加法定理を利用して求めることはできません。
なので、3倍角を利用して求めてみます。
ド・モアブルの定理
\[\cos nθ+i\sin nθ=(\cosθ+i\sinθ)^n\]
より
\begin{align*}\cos 3θ+i\sin
3θ&=(\cosθ+i\sinθ)^3\\[0.5em]&=\cos^3θ+3i\cos^2θ\sinθ-3\cosθ\sin^2θ-i\sin^3θ\\[0.5em]&=(\cos^3θ-3\cosθ\sin^2θ)+i(3\cos^2θ\sinθ-\sin^3θ)\\[0.5em]&=\{\cos^3θ-3\cosθ(1-\cos^2θ)\}\\
&\qquad+i\{3(1-\sin^2θ)\sinθ-\sin^3θ\}\\[0.5em]&=(4\cos^4θ-3\cosθ)+i(3\sinθ-4\sin^3θ)\end{align*}
となるので、
\begin{cases}\cos3θ=4\cos^3θ-3\cosθ\\[0.5em]\sin3θ=3\sinθ-4\sin^3θ\end{cases}
が3倍角の公式となります。
$\sin10°$
正弦の3倍角の公式に$\theta=10°$を代入すると
\begin{align*}\sin30°&=3\sin10°-4\sin^3
10°\\[0.5em]\frac{1}{2}&=3\sin10°-4\sin^3 10°\end{align*}
となります。
ここで$\sin10°=x$とおくと
しかしこの3次方程式は因数分解で解くことができず、3次方程式の解の公式を利用しようにも実数となるはずの解が実数にできない（還元不可能）ため、解の1つは$\sin10°$であるという状態から進めなくなってしまいます。
\begin{align*}\frac{1}{2}&=3x-4x^3\\[0.5em]4x^3-3x+\frac{1}{2}&=0\\[0.5em]8x^3-6x+1&=0\tag{a}\end{align*}
となり、前述よりこの3次方程式の解の1つが$x=\sin10°$であるため、これを解けば$\sin10°$がどういった式で表されるのかがわかるはずです。しかしこの3次方程式は因数分解で解くことができず、3次方程式の解の公式を利用しようにも実数となるはずの解が実数にできない（還元不可能）ため、解の1つは$\sin10°$であるという状態から進めなくなってしまいます。
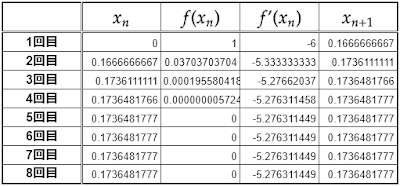
そこで、ニュートン法をもちいて近似解を求めてみます。
$(\text{a})$より$f(x)=8x^3-6x+1$とすると、これの導関数は$f'(x)=24x^2-6$となり、これらを
$(\text{a})$より$f(x)=8x^3-6x+1$とすると、これの導関数は$f'(x)=24x^2-6$となり、これらを
\[x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}\]
にもちいて近似解を求めます。
最初の入力値$x_0$を決定するために$(\text{a})$のもつ解について考えます。
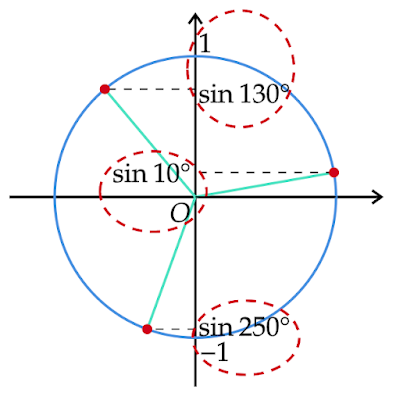
$(\text{a})$は3倍角の公式の3倍角の正弦が$\dfrac{1}{2}$となるときの式がもとになっています。であれば、$\sin10°$以外で3倍角の正弦が$\dfrac{1}{2}$となるような正弦もまた解にもつはずです。
そこで、左辺の$3θ=30°$を$3θ=30°+360°×n$の一般角に置き換えると$θ$は
\[x=\sin10°,\sin130°,\sin250°\]
の3つとなることがわかります。
\begin{align*}n=0のとき\\ θ&=30°\\[1em]n=1のとき\\
θ&=\frac{30°+360°}{3}=130°\\[1em]n=2のとき\\
θ&=\frac{30°+720°}{3}=250°\end{align*}
となることから、$(\text{a})$の解は$0°\leqqθ<360°$の範囲において\[x=\sin10°,\sin130°,\sin250°\]
の3つとなることがわかります。
収束した値は反復4回目以降の$x_{n+1}=0.1736481777$でこれが(a)の近似解であり、$\sin10°$の近似値です。
$\cos10°$
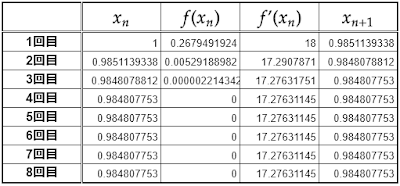
同様に$\cos10°$についても調べてみます。
省略しますが3次方程式は$8x^2-6x-\sqrt{3}=0$なので
\[f(x)=8x^3-6x-\sqrt{3},f'(x)=24x^2-6\]
となります。$\cos10°$は$1$に近い値を持つので入力する$x$の値は$x_0=1$です。
近似解は$x=0.984807753$でこれが$\cos10°$の近似値となります。
また、
\[\cos10°=\sqrt{1-\sin^2 10°}\]
で求めても同様の値を得ることができます。
$\tan10°$
$\tanθ$の3倍角の公式は
\[\tan3θ=\frac{\tan^3θ-3\tanθ}{3\tan^2θ-1}\]
なので、$θ=10°$を代入し、$\tan10°=x$とおくと
\[\frac{1}{\sqrt{3}}=\frac{x^3-3x}{3x^2-1}\]
となります。
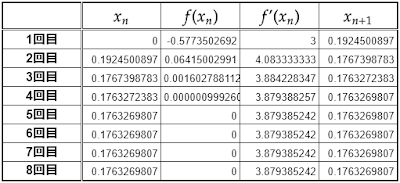
したがって、使用する関数は
\[f(x)=\frac{x^3-3x}{3x^2-1}-\frac{1}{\sqrt{3}},f'(x)=\frac{3x^4+6x^2+3}{9x^4-6x^2+1}\]
で、$\tan10°$は$0$に近い値を持つので入力する$x$の値は$x_0=0$です。
近似解$x=0.1763269807$が$\tan10°$の近似値となります。
また、先ほど求めた$\sin10°,\cos10°$の近似値をもちいて
\[\tan10°=\frac{\sin10°}{\cos10°}\]
を計算することでも同様の値を得ることができます。
外部リンク：ニュートン法 - Wikipedia
Share:
