円の接線の方程式の公式

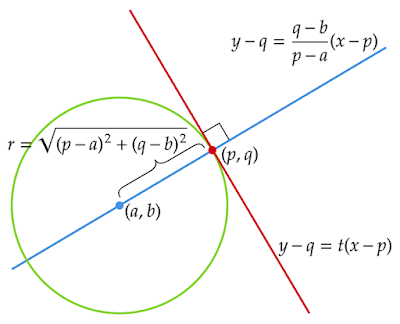
　円$(x-a)^2+(y-b)^2=r^2$の円周上の点$(p,q)$を通る接線の方程式は

$$\large(p-a)(x-a)+(q-b)(y-b)=r^2$$

となります。

なぜこれが円の接線の方程式となるのでしょうか？

　点$(p,q)$を通る接線の方程式は傾きを$t$とおいて

$$y-q=t(x-p)\tag{i}$$

円の中心$(a,b)$と$(p,q)$を通る直線の方程式は

$$y-q=\frac{q-b}{p-a}(x-p)\tag{ii}$$

となります。

ここで、$\text{(i)}$と$\text{(ii)}$は互いに垂直なので

$$t\cdot\frac{q-b}{p-a}=-1$$

となるから$t$は

$$t=-\frac{p-a}{q-b}$$

です。これを$\text{(i)}$に代入すると

$$\begin{align*}y-q&=-\frac{p-a}{q-b}(x-p)\\[0.5em](q-b)(y-q)&=-(p-a)(x-p)\\[0.5em](p-a)(x-p)+(q-b)(y-q)&=0\end{align*}$$

これを変形して

$$\begin{align*}(p-a)\{x-p+(p-a)-(p-a)\}\quad&\\ +(q-b)\{y-q+(q-b)-(q-b)\}&=0\\[0.5em](p-a)\{(x-a)-(p-a)\}+(q-b)\{(y-b)-(q-b)\}&=0\\[0.5em](p-a)(x-a)+(q-b)(y-b)&=(p-a)^2+(q-b)^2\end{align*}$$

ここで円の中心$(a,b)$と$(p,q)$の距離、すなわち半径$r$は

$$\begin{align*}r&=\sqrt{(p-a)^2+(q-b)^2}\\[0.5em]r^2&=(p-a)^2+(q-b)^2\end{align*}$$

であるから、円$(x-a)^2+(y-b)^2=r^2$の円周上の点$(p,q)$を通る接線の方程式は

$$\large(p-a)(x-a)+(q-b)(y-b)=r^2$$

となることがわかります。

関連：円の方程式を円の接線の方程式の公式を利用して求める

旺文社

数学Ⅱ・B基礎問題精講 五訂版

Amazonで見る楽天市場で見るYahoo!ショッピングで見る