不等号が2つある2次不等式を解く

  $$\Large -8\leqq x^2+6x\leqq16$$

「上の不等式を解け。」

　この不等式は$-8\leqq x^2+6x$かつ$x^2+6x\leqq16$というように書くことができるので、
$$\left\{\begin{aligned}&-8\leqq x^2+6x&\cdots(1)\\ &x^2+6x\leqq16&\cdots(2)\end{aligned}\right.$$
という連立不等式にして解きます。

(1)$-8\leqq x^2+6x$

$$\begin{align*}x^2+6x&\geqq-8\\ \\ x^2+6x+8&\geqq0\\ \\ (x+2)(x+4)&\geqq0\end{align*}$$

(1)はさらに$y=(x+2)(x+4)$かつ$y\geqq0$と書けます。

これを満たすのは上のグラフの赤線部分でこれが存在する$x$の範囲

$$x\leqq-4,-2\leqq x\qquad\cdots(3)$$

が(1)の解となります。

(2)$x^2+6x\leqq16$

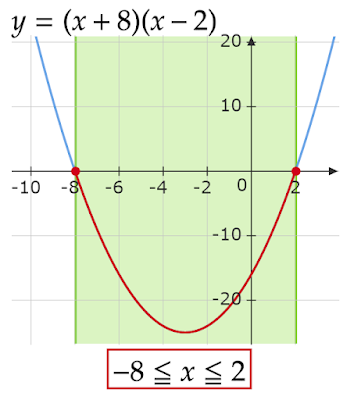
$$\begin{align*}x^2+6x-16&\leqq0\\ \\ (x+8)(x-2)&\leqq0\end{align*}$$

(2)はさらに$y=x^2+6x-16$かつ$y\leqq0$と書けます。

これを満たすのは上のグラフは赤線部分で、これが存在する$x$の範囲

$$-8\leqq x\leqq2\qquad\cdots(4)$$

が(2)の解となります。

　不等式の解は(3)、(4)をともに満たす$x$の範囲なので

紫で示した部分の$-8\leqq x\leqq-4,-2\leqq x\leqq2$となります。

関連：2次不等式を解く(2)