円順列・数珠順列

円順列

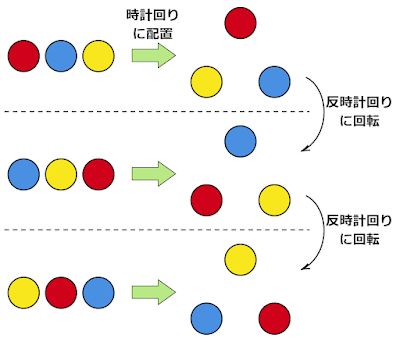
　例として赤色、青色、黄色の球1個ずつを円状に並べるときを考えます。

この3つの球を一列に並べる方法は$3!=6$通りあります。こうして一列に並べた球を円状に並べ直すと回転させて向きを変えただけのように見える並べ方があることに気づきます。

一列に並べたときと違い円状に並べると端がなくなる（列の先頭がなくなる）ため、向きを変えただけの並べ方はすべて同じものとみなすことができます。
向きを変えただけの並べ方は並べた個数分だけ存在するので、一列で並べた場合の並べ方の数を並べた個数で割ります。

例の場合、赤、青、黄の球を1個ずつ円状に並べる並べ方は

\[\frac{3!}{3}=\frac{6}{3}=2\]

となります。

　これを一般化すると、$n$個の球を円状に並べる並べ方は

\[\frac{n!}{n}\]

となりますが、階乗は

\[n!=n×(n-1)×(n-2)×\cdots×2×1\]

であることを考えると、$n$とそれ以降で区切って

\[\frac{n!}{n}=\frac{n×(n-1)!}{n}=(n-1)!\]

とすることができます。

ただし、円状に並べても番号が割り振られているなど並べた場所が区別できる場合は円順列ではなく通常の順列となります。

数珠順列

　数珠順列は円順列のように向きに区別がないことに加え、表裏の区別もありません。

したがって裏返したとき同じ並びになる、つまり同じ面で見たとき鏡像となるような並びが同じものとして取り除かれます。

鏡像となる並べ方は1通りの並べ方に対し1つ存在するので、円順列を$2$で割ることで数珠順列となります。

以上より$n$個の球の数珠順列の求め方は

\[\frac{(n-1)!}{2}\]

となります。

　円順列で向きについて考えているのに向きで区別しない順列なのは矛盾しているのでは？と思うかもしれませんが、通常の順列は向きが決まっているからこそ向きについて考えなくても良かったのです。

数珠順列も表裏について考えるのに表裏の区別がない順列ですが、同様に円順列では表裏が決まっているから裏返すことについて考えなくても良い順列だったのです。