単位円を利用してsinとcosの加法定理を導く

　「三角関数の加法定理」では、$\cos(α-β)=\cosα\cosβ+\sinα\sinβ$のみ単位円をもちいて導きましたが、他の$\sin,\cos$の加法定理も単位円を利用して導いてみます。

$\cos$の加法定理

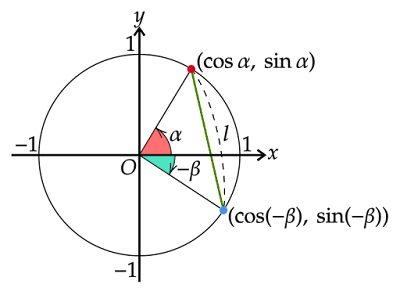
　単位円上の2点$(\cosα,\sinα),\bigl(\cos(-β),\sin(-β)\bigr)$を考えます。
$α$の角を表す動径と$-β$の角を表す動径のなす角は一般角で$α+β$となります。

この2点間の距離$l$の2乗は

$$\begin{align*}l^2&=\bigl\{\cos\alpha-\cos(-\beta)\bigr\}^2+\bigl\{\sin\alpha-\sin(-\beta)\bigr\}^2\\[0.5em]&=\cos^2\alpha-2\cos\alpha\cos(-\beta)+\cos^2(-\beta)\\ &\qquad+\sin^2\alpha-2\sin\alpha\sin(-\beta)+\sin^2(-\beta)\\[0.5em]&=(\sin^2\alpha+\cos^2\alpha)+\bigl\{\sin^2(-\beta)+\cos^2(-\beta)\bigr\}\\ &\qquad-2\bigl\{\cos\alpha\cos(-\beta)+\sin\alpha\sin(-\beta)\bigr\}\\[0.5em]&=2-2\{\cos\alpha\cos(-\beta)+\sin\alpha\sin(-\beta)\}\\ &\qquad(\because\sin^2x+\cos^2x=1)\end{align*}$$

となり、三角関数の性質$\sin(-x)=-\sin x,\cos(-x)=\cos x$より

$$\begin{align*}l^2&=2-2\bigl\{\cos\alpha\cos\beta+\sin\alpha(-\sin\beta)\bigr\}\\[0.5em]&=2-2(\cos\alpha\cos\beta-\sin\alpha\sin\beta)\tag1\end{align*}$$

となります。

関連：$-θ,90°±θ,180°±θ,270°±θ$の三角関数

　次に単位円上の2点$\bigl(\cos(α+β),\sin(α+β)\bigr),(1,0)$を考えます。
$(1,0)$を通る動径が表す角度は$0°$なので、$0°$の角を表す動径と$α+β$の角を表す動径のなす角も一般角では$α+β$であり、2点間の距離も$l$となります。

これら2点の座標をもちいて$l^2$を表すと

$$\begin{align*}l^2&=\{\cos(\alpha+\beta)-1\}^2+\{\sin(\alpha+\beta)-0\}^2\\[0.5em]&=\cos^2(\alpha+\beta)-2\cos(\alpha+\beta)+1\\ &\qquad+\sin^2(\alpha+\beta)\\[0.5em]&=\bigl\{\sin^2(\alpha+\beta)+\cos^2(\alpha+\beta)\bigr\}\\ &\qquad+1-2\cos(\alpha+\beta)\\[0.5em]&=2-2\cos(\alpha+\beta)\tag2\\ &\qquad(\because\sin^2x+\cos^2x=1)\end{align*}$$

となります。

$(1),(2)$より

$$\begin{align*}2-2(\cos\alpha\cos\beta-\sin\alpha\sin\beta)&=2-2\cos(\alpha+\beta)\\[0.5em]\therefore\cos(\alpha+\beta)&=\cos\alpha\cos\beta-\sin\alpha\sin\beta\end{align*}$$

が導かれます。

$\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta$の導出については↓

関連：三角関数の加法定理

$\sin$の加法定理

$\sin(α+β)$

　単位円上の2点$\bigl(\cos(90°-α),\sin(90°-α)\bigr),\bigl(\cosβ,\sinβ\bigr)$を考えます。
$90°-α$の角を表す動径と$β$の角を表す動径のなす角は一般角で$90°-α-β=90°-(α+β)$となります。

この2点間の距離$l$の2乗は

$$\begin{align*}l^2&=\bigl\{\cos(90°-\alpha)-\cos\beta\bigr\}^2+\bigl\{\sin(90°-\alpha)-\sin\beta\bigr\}^2\\[0.5em]&=\cos^2(90°-\alpha)-2\cos(90°-\alpha)\cos\beta+\cos^2\beta\\ &\qquad+\sin^2(90°-\alpha)-2\sin(90°-\alpha)\sin\beta+\sin^2\beta\\[0.5em]&=\bigl\{\sin^2(90°-\alpha)+\cos^2(90°-\alpha)\bigr\}+\bigl\{\sin^2\beta+\cos^2\beta\bigr\}\\ &\qquad-2\bigl\{\cos(90°-\alpha)\cos\beta+\sin(90°-\alpha)\sin\beta\bigr\}\\[0.5em]&=2-2\bigl\{\cos(90°-\alpha)\cos\beta+\sin(90°-\alpha)\sin\beta\bigr\}\\ &\qquad(\because\sin^2x+\cos^2x=1)\end{align*}$$

となり、三角関数の性質$\sin(90°-x)=\cos x,\cos(90°-x)=\sin x$より

$$l^2=2-2(\sin\alpha\cos\beta+\cos\alpha\sin\beta)\tag3$$

となります。

　次に単位円上の2点$\bigl(\cos\{90°-(α+β)\},\sin\{90°-(α+β)\}\bigr),(1,0)$を考えます。
$\cos$の加法定理のときと同様、$0°$の角を表す動径（$(1,0)$を通る動径）と$90°-(α+β)$の角を表す動径のなす角も一般角では$90°-(α+β)$であり、2点間の距離も$l$となります。

これら2点の座標をもちいて$l^2$を表すと

$$\begin{align*}l^2&=\bigl[\cos\{90°-(\alpha+\beta)\}-1\bigr]^2+\bigl[\sin\{90°-(\alpha+\beta)\}-0\bigr]^2\\[0.5em]&=\cos^2\{90°-(\alpha+\beta)\}-2\cos\{90°-(\alpha+\beta)\}+1\\ &\qquad+\sin^2\{90°-(\alpha+\beta)\}\\[0.5em]&=\bigl[\sin^2\{90°-(\alpha+\beta)\}+\cos^2\{90°-(\alpha+\beta)\}\bigr]\\ &\qquad+1-2\cos\{90°-(\alpha+\beta)\}\\[0.5em]&=2-2\cos\{90°-(\alpha+\beta)\}\tag4\\ &\qquad(\because\sin^2x+\cos^2x=1)\end{align*}$$

となります。

$(3),(4)$より

$$\begin{align*}2-2(\sin\alpha\cos\beta+\cos\alpha\sin\beta)&=2-2\cos\{90°-(\alpha+\beta)\}\\[0.5em]\therefore\cos\{90°-(\alpha+\beta)\}&=\sin\alpha\cos\beta+\cos\alpha\sin\beta\end{align*}$$

さらに、三角関数の性質$\cos(90°-x)=\sin x$より

$$\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta$$

となり、$\sin$の加法定理の1つが導かれます。

$\sin(α-β)$

　単位円上の2点$\bigl(\cos(90°-α),\sin(90°-α)\bigr),\bigl(\cos(-β),\sin(-β)\bigr)$を考えます。
$90°-α$の角を表す動径と$β$の角を表す動径のなす角は一般角で$90°-α+β=90°-(α-β)$となります。

この2点間の距離$l$の2乗は

$$\begin{align*}l^2&=\bigl\{\cos(90°-\alpha)-\cos(-\beta)\bigr\}^2+\bigl\{\sin(90°-\alpha)-\sin(-\beta)\bigr\}^2\\[0.5em]&=\cos^2(90°-\alpha)-2\cos(90°-\alpha)\cos(-\beta)+\cos^2(-\beta)\\ &\qquad+\sin^2(90°-\alpha)-2\sin(90°-\alpha)\sin(-\beta)+\sin^2(-\beta)\\[0.5em]&=\bigl\{\sin^2(90°-\alpha)+\cos^2(90°-\alpha)\bigr\}+\bigl\{\sin^2(-\beta)+\cos^2(-\beta)\bigr\}\\ &\qquad-2\bigl\{\cos(90°-\alpha)\cos(-\beta)+\sin(90°-\alpha)\sin(-\beta)\bigr\}\\[0.5em]&=2-2\bigl\{\cos(90°-\alpha)\cos(-\beta)+\sin(90°-\alpha)\sin(-\beta)\bigr\}\\ &\qquad(\because\sin^2x+\cos^2x=1)\end{align*}$$

となり、三角関数の性質$\sin(90°-x)=\cos x,\cos(90°-x)=\sin x,$$\sin(-x)=-\sin x,\cos(-x)=\cos x$より

$$\begin{align*}l^2&=2-2\bigl\{\sin\alpha\cos\beta+\cos\alpha(-\sin\beta)\bigr\}\\[0.5em]&=2-2(\sin\alpha\cos\beta-\cos\alpha\sin\beta)\tag5\end{align*}$$

となります。

　次に単位円上の2点$\bigl(\cos\{90°-(α-β)\},\sin\{90°-(α-β)\}\bigr),(1,0)$を考えます。
$\cos$の加法定理のときと同様、$0°$の角を表す動径（$(1,0)$を通る動径）と$90°-(α-β)$の角を表す動径のなす角も一般角では$90°-(α-β)$であり、2点間の距離も$l$となります。

これら2点の座標をもちいて$l^2$を表すと

$$\begin{align*}l^2&=\bigl[\cos\{90°-(\alpha-\beta)\}-1\bigr]^2+\bigl[\sin\{90°-(\alpha-\beta)\}-0\bigr]^2\\[0.5em]&=\cos^2\{90°-(\alpha-\beta)\}-2\cos\{90°-(\alpha-\beta)\}+1\\ &\qquad+\sin^2\{90°-(\alpha-\beta)\}\\[0.5em]&=\bigl[\sin^2\{90°-(\alpha-\beta)\}+\cos^2\{90°-(\alpha-\beta)\}\bigr]\\ &\qquad+1-2\cos\{90°-(\alpha-\beta)\}\\[0.5em]&=2-2\cos\{90°-(\alpha-\beta)\}\tag6\\ &\qquad(\because\sin^2x+\cos^2x=1)\end{align*}$$

となります。

$(5),(6)$より

$$\begin{align*}2-2(\sin\alpha\cos\beta-\cos\alpha\sin\beta)&=2-2\cos\{90°-(\alpha-\beta)\}\\[0.5em]\therefore\cos\{90°-(\alpha-\beta)\}&=\sin\alpha\cos\beta-\cos\alpha\sin\beta\end{align*}$$

さらに、三角関数の性質$\cos(90°-x)=\sin x$より

$$\sin(\alpha-\beta)=\sin\alpha\cos\beta-\cos\alpha\sin\beta$$

となり、$\sin$の加法定理の1つが導かれます。

関連：三角関数の加法定理

関連：三角関数の読み方　②単位円の利用