正の数のべき乗$a^x$はすべての実数$x$で実数となります。しかし負の数のべき乗$(-a)^x\
(a>0)$はすべての実数$x$で実数となるわけではありません。
$x$が整数のとき
$x=2n\ (n:\text{整数})$、すなわち$x$が偶数のとき
\begin{align*}(-a)^{2n}&=\left\{(-a)^2\right\}^n\\[0.5em]&=(a^2)^n\\[0.5em]&=a^{2n}\end{align*}
となるので、正の実数となります。
$x=0$のときは$x$の偶数のときに含まれますが、$a$の値に関わらず$(-a)^0=1$となります。
$x=2n+1\ (n:\text{整数})$、すなわち$x$が奇数のとき
\begin{align*}(-a)^{2n+1}&=(-a)^{2n}\cdot(-a)\\[0.5em]&=\left\{(-a)^2\right\}^n\cdot(-a)\\[0.5em]&=(a^2)^n\cdot(-a)\\[0.5em]&=a^{2n}\cdot(-a)\\[0.5em]&=-a^{2n+1}\end{align*}
となるので、負の実数となります。
$x$が整数以外の有理数のとき
$x$が$0$以外の整数の逆数の場合から考えます。
$x=\dfrac{1}{2n}\ (n:\text{整数})$、すなわち$x$が偶数の逆数のとき
\begin{align*}(-a)^{\frac{1}{2n}}&=a^{\frac{1}{2n}}\cdot(-1)^{\frac{1}{2n}}\end{align*}
ここで、オイラーの公式をもちいて
\begin{align*}a^{\frac{1}{2n}}\cdot(-1)^{\frac{1}{2n}}&=a^{\frac{1}{2n}}\cdot\left\{e^{i(2m+1)\pi}\right\}^{\frac{1}{2n}}&(m:\text{整数})\\[0.5em]&=a^{\frac{1}{2n}}\cdot
e^{i\frac{2m+1}{2n}\pi}\end{align*}
となります。複素数の範囲まで広げて考えた結果、任意の整数$m$が現れたことで複数の複素数を表す状態となっていますが、$(-a)^x$が実数となる適当な$m$が存在するとき、$(-a)^x$は実数であるとします。
ここで、$a^{\frac{1}{2n}}$は実数なので、$e^{i\frac{2m+1}{2n}\pi}$に実数となるものがあるかを確認します。
$e^{i\frac{2m+1}{2n}\pi}$が実数になるためには、指数部分の$\dfrac{2m+1}{2n}$が整数である必要があります。しかし、これが整数になることはありません。
$\dfrac{2m+1}{2n}$は分母が偶数、分子が奇数の分数なので、積の偶奇に着目すると
\begin{align*}(偶数)\times(偶数)&=(偶数)\\[1em](偶数)\times(奇数)&=(偶数)\\[1em](奇数)\times(奇数)&=(奇数)\end{align*}
より、分母は$(偶数)\times(偶数)$、または$(偶数)\times(奇数)$からなり、分子は$(奇数)\times(奇数)$からなるということになります。
すると$\dfrac{2m+1}{2n}$はすでに既約分数で整数にならないか、奇数が共通因数となり約分できる可能性はあっても結局$(奇数)/(偶数)$の形のままで整数にならないかのどちらかです。
したがって、$n$に対しどのように$m$をとっても$e^{i\frac{2m+1}{2n}\pi}$が実数とならないので、$(-a)^{\frac{1}{2n}}$もまた実数となりません。
また、$(-a)^{\frac{1}{2n}}$の累乗、すなわち整数$k$をもちいて
\begin{align*}\left\{(-a)^{\frac{1}{2n}}\right\}^k&=\left\{a^{\frac{1}{2n}}\cdot
e^{i\frac{2m+1}{2n}\pi}\right\}^k\\[0.5em]&=a^\frac{k}{2n}\cdot
e^{i\frac{k(2m+1)}{2n}\pi}\end{align*}
の$\dfrac{k(2m+1)}{2n}$が整数のとき実数になります。そのときの$k$の条件は$2n$の倍数であることですが、それは結局$-a$の整数乗に他なりません。
したがって、$x$が分母が偶数の有理数であるとき、$(-a)^x$が実数となるものは存在しません。
$x=\dfrac{1}{2n+1}\ (n:\text{整数})$、すなわち$x$が奇数の逆数のとき
\begin{align*}(-a)^{\frac{1}{2n+1}}&=a^{\frac{1}{2n+1}}\cdot(-1)^{\frac{1}{2n+1}}\\[0.5em]&=a^{\frac{1}{2n+1}}\cdot\left\{e^{i(2m+1)\pi}\right\}^{\frac{1}{2n+1}}&(m:\text{整数})\\[0.5em]&=a^{\frac{1}{2n+1}}\cdot
e^{i\frac{2m+1}{2n+1}\pi}\end{align*}
となります。
ここで、$a^{\frac{1}{2n+1}}$は実数なので、$e^{i\frac{2m+1}{2n+1}\pi}$に実数となるものがあるかを確認します。
$e^{i\frac{2m+1}{2n+1}\pi}$が実数となるためには、指数部分の$\dfrac{2m+1}{2n+1}$が整数である必要があります。
分母と分子ともに奇数なので上記の積の偶奇の$(奇数)\times(奇数)$より、分子が分母の奇数倍のとき、約分できかつ整数となります。すなわち整数$k$をもちいて$2m+1=(2k+1)(2n+1)$となれば$\dfrac{2m+1}{2n+1}=2k+1$なので、
\[e^{i\frac{2m+1}{2n+1}\pi}=e^{i(2k+1)\pi}=-1\]
です。
したがって、$e^{i\frac{2m+1}{2n+1}\pi}$が実数となるような$m$が存在し、かつ$e^{i\frac{2m+1}{2n+1}\pi}=-1$になるので、$(-a)^{\frac{1}{2n+1}}$は負の実数となります。
またこのことから、$(-a)^{\frac{1}{2n+1}}$の累乗は$x$が整数の場合と同じ場合分けとなります。
すなわち整数$m$をもちいて、指数の分子が偶数の$(-a)^{\frac{2m}{2n+1}}$は正の実数、分子が奇数の$(-a)^{\frac{2m+1}{2n+1}}$は負の実数となります。
$x$が分母が奇数の有理数のときの場合分けは、上記の$(-a)^{\frac{2m+1}{2n+1}}$の指数部分$\dfrac{2m+1}{2n+1}$が整数となるときを除いたものとなります。
$x$が整数のときと整数以外の有理数のときで$x$が任意の有理数の場合を考えることができました。
$x$が無理数のとき
\begin{align*}(-a)^x&=(-1\cdot a)^x\\[0.5em]&=(-1)^x\cdot
a^x\\[0.5em]&=e^{ix(2m+1)\pi}\cdot a^x&(m:\text{整数})\end{align*}
より、$a^x$は実数であるので、$e^{ix(2m+1)\pi}$に実数となるものがあれば$(-a)^x$は実数であるといえます。
$x$が既約分数の時と同様に$e^{ix(2m+1)\pi}$の指数部分のうち$x(2m+1)$が整数のとき、$(-a)^x$も実数となります。しかし、$x$は無理数、$2m+1$は整数なので、$x(2m+1)$は無理数です。
したがって、$x$が無理数のとき$e^{ix(2m+1)\pi}$は実数とならないので$(-a)^x$もまた実数になりません。
以上をまとめると以下のようになります。
$x$が有理数のとき
└$x$が整数のとき
└$x$が整数以外の有理数のとき
└$x$が分母が偶数の有理数のとき、$(-a)^x$は虚数
$x$が無理数のとき、$(-a)^x$は虚数
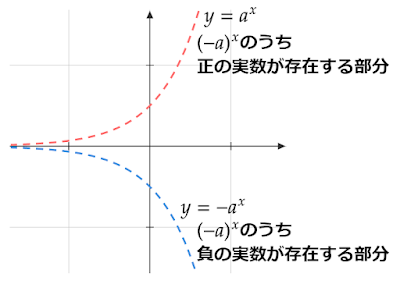
$y=(-a)^x$のグラフを座標平面に描こうとすると線となる部分はなく点のみとなります。この無数にある点を1つ1つ丁寧に打って描き表すのは非常に困難ですが、点がどのあたりに存在しているのかというのは以下のグラフのように示すことはできます。
\[(-a)^x=e^{ix(2m+1)\pi}\cdot a^x\quad(m:\text{整数})\]
と書け、$x$によらず常に$\left|e^{ix(2m+1)\pi}\right|=1$であることから、$\left|(-a)^x\right|=\left|a^x\right|$となります。
したがって、座標平面上の$y=(-a)^x$を満たす点は$y=a^x$または$y=-a^x$のグラフ上に存在することがわかります。
Share:
https://p-suugaku.blogspot.com/2023/05/funosuu-bekijou.html負の数のべき乗が実数となる条件は?