tanのとりうる値の範囲はなぜすべての実数なのか？

 　任意の実数$θ$において$\tanθ$のとりうる値の範囲はなぜすべての実数なのでしょうか？

　$\tanθ$の単位円による定義は、始線と反時計回りに$θ$の角をなす半径を延長した直線の傾きであり、半径の延長と直線$x=1$の交点のy座標でした。

本記事では後者を利用して$\tanθ$の値の範囲がすべての実数となることを確かめてみます。

関連：三角関数の読み方　②単位円の利用

　$-\dfrac{\pi}{2}<θ<\dfrac{\pi}{2}$の区間に限定して$\tanθ$の値について考えます。

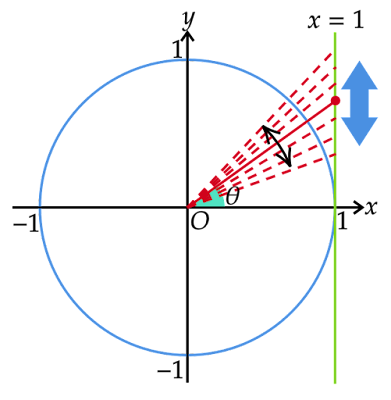
　$θ$をなめらかに変化させてみると半径の延長と直線$x=1$の交点は直線$x=1$上をなめらかに移動します。すなわち、$\tanθ$の値を表す交点のy座標がなめらかに変化します。
これは$\tanθ$のとりうる値の範囲には途切れている部分がなく1つの区間で表せることを意味します。

　$0\leqqθ<\dfrac{\pi}{2}$のとき$\tanθ$の値は$0$以上です。$θ$を$\dfrac{\pi}{2}$に近づけていくと半径の延長と直線$x=1$の交点のy座標は大きくなっていきます。
この交点のy座標は$θ$を$\dfrac{\pi}{2}$に近づければ近づけるほど際限なく大きくなっていきます。

　$-\dfrac{\pi}{2}<θ\leqq0$のとき$\tanθ$の値は$0$以下です。$θ$を$-\dfrac{\pi}{2}$に近づけていくと半径の延長と直線$x=1$の交点のy座標は小さくなっていきます。
この交点のy座標は$θ$を$-\dfrac{\pi}{2}$に近づければ近づけるほど際限なく小さくなっていきます。

以上より$\tanθ$の値は際限なく大きくもなり小さくもなる、すなわち最大値・最小値が存在しないことがわかります。

　$\tanθ$のとりうる値の範囲には最大値・最小値がなく、かつ途切れている部分がななく1つの区間で表せるということは、$0$より大きい数も小さい数も無数に存在する実数のどのような値もとれるということであるため、$-\dfrac{\pi}{2}<θ<\dfrac{\pi}{2}$における$\tanθ$の値のとりうる値の範囲はすべての実数となります。

$-\dfrac{\pi}{2}<θ<\dfrac{\pi}{2}$を任意の実数$θ$に置き換えても、上述したことからやはり$\tanθ$のとりうる値の範囲はすべての実数となります。

また、上述したことは$\dfrac{2n-1}{2}\pi<θ<\dfrac{2n+1}{2}\pi$（$n$：整数）においても同様です。

際限なく大きくなる（小さくなる）という点に関しては、$θ=\dfrac{2n-1}{2}\pi$（または$θ=\dfrac{2n+1}{2}\pi$）へ第1象限または第3象限から近づいたとき$\tanθ$の値は際限なく大きくなり、第2象限または第4象限から近づいたとき$\tanθ$の値は際限なく小さくなります。