4つに分割された長方形の一部分の面積は？

「上の(1)、(2)はそれぞれ長方形を4つに分割している。
分割された図形の内部の数字はその図形の面積である。？の部分の面積を求めよ。」

このような問題はどのように解けばよいのでしょうか？

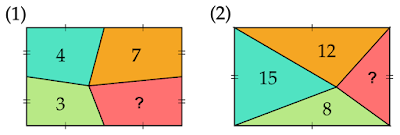
(1)

　長方形を分割している4本の線分の交点から長方形の頂点へ線分を引くと上図のように8つの三角形に分割されます。
このとき、長方形の1辺のほうを底辺としてみると、同じ色で塗られている三角形は底辺の長さは長方形の同じ辺の半分の長さであるため等しく、高さも等しいので面積が等しいことがわかります。

　ここで、上述の三角形の面積の特徴とそれぞれの四角形がどの三角形の面積の和となっているかに着目すると求める右下の四角形の面積は

\[(右下の四角形)=(左下の四角形)+(右上の四角形)-(左上の四角形)\]

で求められることがわかるので、それぞれの四角形の面積に置き換えると

\begin{align*}?&=3+7-4\\[0.5em]&=6\end{align*}

となり、右下の四角形の面積が$6$であるとわかります。

　これを文字を利用して解くと以下のようになります。

青、緑、赤、黄色の三角形の面積をそれぞれ$w,x,y,z$とおくと、問題の四角形の面積はそれぞれ

\begin{cases}w+x=4\\[1em]x+y=3\\[1em]w+z=7\\[1em]y+z=?\end{cases}

と書けます。

ここで、上の4式から$y+z$が

\[y+z=(x+y)+(w+z)-(w+x)\]

で求められることがわかるので、それぞれ代入すると

\begin{align*}?&=3+7-4\\[0.5em]&=6\end{align*}

となります。

(2)

　上図のように長方形の横の長さを$X$、縦の長さを$Y$とし、4つの三角形の高さをそれぞれ$a,b,c,d$とします。このとき、長方形の対辺、$a,b$の線分と長方形の横の辺、$c,d$の線分と縦の辺はそれぞれ平行なので、$a+b=X,c+d=Y$です。

長方形の横の辺を1辺とする2つの三角形の面積の和を求めてみると

\begin{align*}\frac{1}{2}cX+\frac{1}{2}dX&=\frac{1}{2}(c+d)X\\[0.5em]&=\frac{1}{2}XY\end{align*}

となるので、長方形の面積の半分であることがわかります。

また、長方形の縦の辺を1辺とする2つの三角形の面積の和を求めてみると

\begin{align*}\frac{1}{2}aY+\frac{1}{2}bY&=\frac{1}{2}(a+b)Y\\[0.5em]&=\frac{1}{2}XY\end{align*}

となるので、こちらも長方形の面積の半分となります。

このことから、対辺を1辺とする三角形同士の面積の和は等しいので

\[12+8=15+?\]

という関係があることがわかります。
これを解くと

\begin{align*}20&=15+?\\[0.5em]?&=5\end{align*}

となります。

　対辺を1辺とする三角形同士の面積の和が長方形の面積の半分となることは等積変形からもわかります。

長方形の横の辺を1辺とする2つの三角形は上図のように三角形の対辺に平行な直線に沿って頂点を動かして等積変形します。
すると、長方形を1本の対角線で分割してできる直角三角形に変形できます。この直角三角形の面積は長方形の面積の半分なので、長方形の横の辺を1辺とする2つの三角形の面積の和も長方形の面積の半分であることがわかります。

関連：三角形の等積変形

長方形の横の辺を1辺とする2つの三角形は上図のように三角形の対辺に平行な直線に沿って頂点を動かして等積変形します。
こちらも同じ直角三角形に変形できます。したがって、長方形の縦の辺を1辺とする2つの三角形の面積の和も長方形の面積の半分であることがわかります。