2024年12月30日
リサジュー図形とは?
2024年12月23日
互いに素でない2数に関する命題の真偽は?
(1)$a$と$b$が互いに素でないならば$a$は$b$の倍数である
(2)$a$と$p$が互いに素でないならば$a$は$p$の倍数である」2024年12月19日
フェルマーの小定理
これが成り立つことを確かめてみます。
2024年12月18日
ウィルソンの定理とその逆
これが成り立つことを確かめてみます。
2024年12月17日
ある素数未満の自然数の倍数をある素数で割ったときの余りの性質
これが成り立つことを確かめてみます。
2024年12月15日
倍数を互いに素な自然数で割ったときの余りの性質
$A,2A,\cdots,(B-1)A,BA$をそれぞれ$B$で割ったときの余りを一列に並べたものは$0,1,\cdots,B-2,B-1$の並び替えである
これが成り立つことを確かめてみます。
2024年12月9日
関数のグラフを伸び縮みさせる
2024年12月6日
微分係数の定義式を利用して証明する問題
これをもちいて以下の式が成り立つことを証明せよ。
2024年11月29日
座標平面上の点の平行移動・対称移動
| ○○ | 平行移動の結果 |
|---|---|
| x軸方向へ$p$ | $(\textcolor{red}{a+p},b)$ |
| y軸方向へ$q$ | $(a,\textcolor{red}{b+q})$ |
| x軸方向へ$p$ y軸方向へ$q$ |
$(\textcolor{red}{a+p}, \textcolor{blue}{b+q})$ |
| ○○ | 対称移動の結果 |
|---|---|
| x軸 | $(a,\textcolor{red}{-b})$ |
| y軸 | $(\textcolor{red}{-a},b)$ |
| 原点 | $(\textcolor{red}{-a},\textcolor{blue}{-b})$ |
| 直線$x=p$ | $(\textcolor{red}{2p-a},b)$ |
| 直線$y=q$ | $(a,\textcolor{red}{2q-b})$ |
| 点$(p,q)$ | $(\textcolor{red}{2p-a},\textcolor{blue}{2q-b})$ |
| 直線$y=x$ | $(\textcolor{red}{b},\textcolor{blue}{a})$ |
なぜこのようになるのかを考えます。
2024年11月21日
1次関数y=ax+bはy=axをy軸方向へ平行移動したものでしかない?
「1次関数(グラフの形、傾き、y切片)」にて、1次関数$y=ax+b$($a,b:$実数、$a\neq0$)は同じ1次関数の$y=ax$をy軸方向に$b$だけ平行移動したものであると説明しましたが、y軸方向のみへの平行移動の場合でしか$y=ax+b$の形をとれないのでしょうか?
2024年11月18日
通る2点の座標がわかっている直線の方程式
なぜこの式で表すことができるのでしょうか?
通る点の座標と傾きがわかっている直線の方程式
2024年11月17日
1次関数とは?(グラフの形、傾き、y切片)
2024年11月7日
約分・通分とは?
約分
約分とは、分数の分母と分子を同じ数で割ってより簡単な分数に直すことです。
より簡単な分数とは、より小さい自然数をもちいて表される分数のことです。
2024年10月25日
符号を考慮した長さとは?
2024年10月22日
座標空間内の2点間の距離
なぜこのように表すことができるのかを考えてみます。
2024年10月20日
座標平面上の2点間の距離
なぜこのように表すことができるのかを考えてみます。
2024年10月17日
数直線上の2点間の距離
数直線上に座標が$a,b$である点$\text{A, B}$をとると、2点$\text{A, B}$間の距離$\text{AB}$は
なぜこのように表すことができるのかを考えてみます。
2024年10月10日
三角形の傍心
2024年10月8日
2直線がつくる角の二等分線と2直線を接線とする円の中心
このことを確かめてみます。
2024年10月2日
偶関数・奇関数とは?
偶関数
2024年10月1日
三角形の内角と内心・外心と頂点を結んでできる角の関係を調べる
三角形の1つの内角とその三角形の内心または外心と他の頂点を結んだときにできる角の大きさにはどのような関係があるでしょうか?
2024年9月29日
四平方の定理(ド・グアの定理)
これが成り立つことを確かめてみます。
2024年9月27日
三角形の外心・内心と角度
2024年9月23日
√2^√2^√2^√2^…はどんな値をもつか?
2024年9月21日
二等辺三角形から30°-60°-90°の直角三角形の3辺の比が求まるまで
ただし、三角形の内角の和や三角形の合同、三平方の定理はすでにわかっているものとします。
2024年9月19日
正六角形の1辺の長さや対角線の長さから面積を求める公式をつくってみる
正六角形の面積を1辺の長さや対角線の長さから求める公式はどのようなものでしょうか?
2024年9月14日
台形の4辺の長さから面積を求める公式
なぜこれで台形$\text{ABCD}$の面積が求められるのでしょうか?
2024年9月8日
垂線で分割された三角形の辺の一部の長さは?
2024年8月30日
正十二角形の面積を求める
2024年8月21日
直線上の点をベクトルで表すと
座標平面上の直線$l:y=ax+b$($a,b:$実数)上の任意の点$\text{P}$を位置ベクトル$\vec{p}$をもちいて表す方法について考えてみます。
2024年8月16日
微分係数をもたない例を挙げてみる
$\lim_{x\to c-0}f(x)$は$x$を$c$より小さい値から$c$に限りなく近づける左側極限、$\lim_{x\to c+0}f(x)$は$x$を$c$より大きい値から$c$に限りなく近づける右側極限です。
2024年8月12日
平均変化率とは?
平均変化率とは、$x$の変化量に対する$y$の変化量の割合、言い換えれば$x$の増加量$1$あたりの$y$の変化量のことです。変化の割合ともいいます。
2024年8月11日
なぜ連続関数は定義域の端で微分係数をもたないのか?
$a\leqq x\leqq b$で定義されている連続関数$y=f(x)$の微分係数を調べると$x=a$と$x=b$における微分係数がありません。
2024年8月6日
食塩水の濃度と重さの問題
「濃度が$3$%の食塩水$200$gを加熱して水分をいくらか蒸発させた。
加熱後の食塩水の濃度を調べてみると$4$%であった。この$4$%食塩水の重さを求めよ。」
2024年8月1日
放物線上の点の作図
2024年7月30日
複素数平面上の3点がつくる角の大きさ
なぜこれで求めることができるのでしょうか?
2024年7月24日
2024年7月21日
2024年7月14日
ベクトルの成分とは?
ベクトルの成分とは、あるベクトルを始点が原点となるように平行移動したときの終点の座標のことです。
2024年7月13日
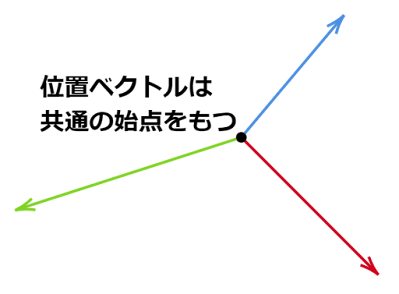
位置ベクトルとは?
2024年7月7日
2024年7月3日
台形の中の三角形の面積は?(等積変形・相似比・面積比)
2024年7月1日
x軸を回転軸とする回転体の体積と定積分
なぜこれで求めることができるのでしょうか?
2024年6月27日
球の中心からどのくらい離れた平面で切断すれば球の1/4の体積の立体を切り取れるか?
球を平面で2つの立体に切断して、そのうちの1つの立体の体積が球の体積の$\dfrac{1}{4}$となるとき、切断する平面は球の中心からどのくらい離れた位置にあるでしょうか?
2024年6月21日
直線と平面が平行であるとは?
2024年6月19日
直線と平面が垂直であるとは?
2024年6月14日
2次方程式を解く ②因数分解を利用する
2次方程式は因数分解を利用して解くことができます。
2次方程式を解く ①平方根として求める
2次方程式の解を平方根として求めることができます。
2024年6月9日
なぜa+(-b)=a-b、a-(-b)=a+bとなるのかを数直線で考える
2024年5月29日
体積を2等分できる円錐の底面に平行な面はどこにある?
円錐を底面と平行な面で2つの立体に切り分けてそれぞれの立体の体積が等しくなるとき、円錐とその面の位置関係はどのようになっているでしょうか?
2024年5月21日
碁盤の目状の道路網の各交差点にたどり着く確率を求める
2024年5月16日
碁盤の目状の道路網の確率(2)
2024年5月11日
碁盤の目状の道路網の確率
2024年5月6日
平面座標を三角関数をもちいて表す 例題
(2)$\large(7,-7)$
(3)$\large\left(-2,-\dfrac{2}{\sqrt{3}}\right)$」
2024年5月3日
平面座標から三角関数の合成の公式を導く
三角関数の合成の公式を平面座標を利用して導いてみます。
2024年4月26日
単位円を利用してsinとcosの加法定理を導く
「三角関数の加法定理」では、$\cos(α-β)=\cosα\cosβ+\sinα\sinβ$のみ単位円をもちいて導きましたが、他の$\sin,\cos$の加法定理も単位円を利用して導いてみます。
2024年4月20日
平面座標を三角関数をもちいて表す
なぜこのように表すことができるのでしょうか?2通りの方法で確かめてみます。
2024年4月17日
垂線の作図法
点$\text{P}$を通る直線$l$の垂線を定規とコンパスを使って作図する方法を、点$\text{P}$が直線$l$上にある場合とない場合の2通り紹介します。
2024年4月10日
不等式と「かつ」と「または」
(2)$x=3$または$x>3$
(3)$x>-1$かつ$x\geqq3$
(4)$x>-1$または$x\geqq3$
(5)$3\leqq x\leqq7$かつ$x>7$
(6)$3\leqq x\leqq7$または$x>7$」
2024年4月8日
極座標から直交座標への変換 直交座標から極座標への変換
極座標から直交座標、直交座標から極座標への変換はどのようにするのでしょうか?
2024年4月4日
素数判定と素因数分解 例題
(1)$191$
(2)$259$
(3)$101$」2024年3月31日
なぜ素数であるかを平方根以下の素数を約数としてもつかで判定できるのか?
自然数$n$が素数であるかはなぜ$\sqrt{n}$以下の素数を約数としてもつかどうかで判定できるのでしょうか?
2024年3月29日
極座標とは
2024年3月20日
小3のテストで出たらしい問題の解説をしてみる
2024年3月14日
正方形に外接する円と半円の面積の関係を調べる
同じ正方形に外接する円と半円の面積にはどのような関係があるでしょうか?
2024年3月11日
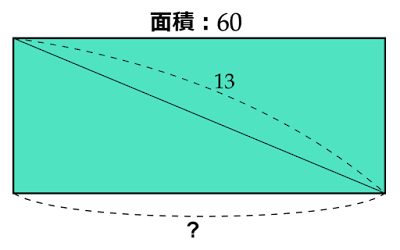
長方形の面積と対角線の長さから1辺の長さを求める
2024年3月8日
直交座標と極座標
直交座標と極座標はどちらも位置を表す方法ですが、これらはどのような違いがあるでしょうか?
2024年2月25日
2024年2月23日
同一直線である条件は?
「相異なる3点$O,A,B$とこれらの点を通らない直線$l$を考える。
2点$O,A$を通る直線と直線$l$との交点と2点$O,B$を通る直線と直線$l$との交点が同一の点であるとき、$O,A$を通る直線と$O,B$を通る直線が同一であることを示せ。」
2024年2月15日
正の数a、bについてa<bと√a<√bは同値?
正の数$a,b$について$a<b$ならば$\sqrt{a}<\sqrt{b}$は成り立つでしょうか?また、その逆は成り立つでしょうか?
2024年2月14日
長方形の各頂点と任意の点を結ぶ線分の長さの関係
長方形の各頂点と任意の点を結ぶ4本の線分の長さにはどのような関係があるでしょうか?
2024年2月11日
有向線分とベクトルの違いは?
2024年2月6日
定積分の値が負の値になることがあるのはなぜなのか?
定積分$\int_a^b{f(x)}dx$はなぜ負の値になることがあるのでしょうか?
2024年1月30日
最大公約数について 間違っているのはどれ?
$\text{(i)}\ \text{gcd}(a,b)$の最大値は$a$である。
$\text{(ii)}\ \text{gcd}(a,b)$のとりうる値には$a<\text{gcd}(a,b)\leqq b$を満たすものが存在する。
$\text{(iii)}\ \text{gcd}(a,b)=1$であることと$a,b$は互いに素であることは同値である。
$\text{(iv)}\ \text{gcd}(a,b)=a$ならば$b$は$a$の倍数である。
2024年1月25日
解が等式でない方程式
2024年1月23日
2024年1月19日
数列の和と因数分解公式
(1)$a_i=p^{n-i}q^{i-1}$とする。(ただし、$n:自然数,p^{-1}q\neq1$)
$S=\sum_{j=1}^n{a_i}$
(2)$a_i=p^{2(n-i)}q^{2(i-1)},b_i=p^{2(n-i)-1}q^{2i-1}$とする。(ただし、$n:自然数,p^{-1}q\neq1$)
$S=\sum_{j=1}^n{a_i}-\sum_{j=i}^{n-1}{b_i}$」
2024年1月13日
座標平面上の分点の座標 ②外分点の座標
座標平面上の分点の座標 ①内分点の座標
2024年1月10日
座標平面上の線分の中点の座標を求める
2024年1月5日
円に内接する四角形の面積は?(余弦定理・トレミーの定理)
「$\text{AB}=\text{BC}=6,$ $\text{BD}=8,$ $∠\text{ABC}=90°$である円に内接する四角形$\text{ABCD}$がある。四角形$\text{ABCD}$の面積を求めよ。」
2024年1月2日
「少なくとも1つは〇〇である」の否定は?
(2) (1)の答えを満たすカードの引き方は何通りか?」
.png)





















.png)





