座標平面上の分点の座標 ①内分点の座標

　座標平面の2点$\text{A}(a_1, a_2), \text{B}(b_1, b_2)$を結ぶ線分$\text{AB}$を$m:n$に内分する点$\text{P}(p_1, p_2)$の$p_1, p_2$はそれぞれ$a_1, a_2, b_1, b_2$をもちいてどのように表されるでしょうか？

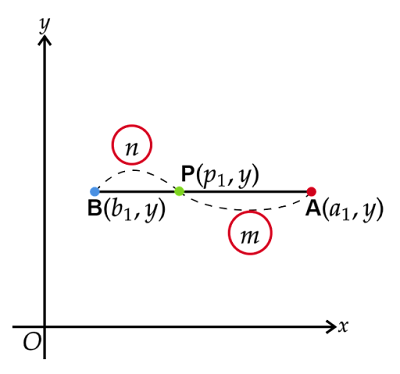
1. 線分$\text{AB}$がx軸に平行な場合

　線分$\text{AB}$がy軸に平行な場合、3点$\text{A, B, P}$のy座標は等しくなります。すなわち、$a_2=b_2=p_2$の場合です。ここではy座標を$y$とおきます。
このとき線分$\text{AB}$の長さは線分の両端の2点$\text{A, B}$それぞれのy座標の差分の絶対値で求められるので$|b_1-a_1|$となります。

すると、線分$\text{AP}$の長さは

\[\text{AP}=\frac{m}{m+n}|b_1-a_1|\]

線分$\text{BP}$の長さは

\[\text{BP}=\frac{n}{m+n}|b_1-a_1|\]

と表すことができます。

$a_1<b_1$のとき

　$a_1<b_1$のとき、点$\text{A, B}$の位置関係は上図と同様であり、線分$\text{AB}$の長さは$|b_1-a_1|=b_1-a_1$と表されます。

点$\text{P}$は点$\text{A}$からx軸方向に線分$\text{AP}$の長さの分だけ平行移動した先にあるため、点$\text{P}$のx座標は

\begin{align*}p_1&=a_1+\frac{m}{m+n}|b_1-a_1|\\[0.5em]&=a_1+\frac{m}{m+n}(b_1-a_1)\\[0.5em]&=\frac{(m+n)a_1+m(b_1-a_1)}{m+n}\\[0.5em]&=\frac{mb_1+na_1}{m+n}\end{align*}

すなわち、点$\text{P}$の座標は

\[(p_1, p_2)=\left(\frac{mb_1+na_1}{m+n}, y\right)\]

と表すことができます。

$a_1>b_1$のとき

　$a_1>b_1$のとき、点$\text{A, B}$の位置関係は上図のようになり、線分$\text{AB}$の長さは$|b_1-a_1|=a_1-b_1$と表されます。
点$\text{P}$は点$\text{B}$からx軸方向に線分$\text{BP}$の長さの分だけ平行移動した先にあるため、点$\text{P}$のx座標は

\begin{align*}p_1&=b_1+\frac{n}{m+n}|b_1-a_1|\\[0.5em]&=b_1+\frac{n}{m+n}(a_1-b_1)\\[0.5em]&=\frac{(m+n)b_1+n(a_1-b_1)}{m+n}\\[0.5em]&=\frac{mb_1+na_1}{m+n}\end{align*}

すなわち、点$\text{P}$の座標は

\[(p_1, p_2)=\left(\frac{mb_1+na_1}{m+n}, y\right)\]

と表すことができます。

　以上より、点$\text{A, B}$のx座標の大小関係がどのようであってもx軸に平行な線分$\text{AB}$を$m:n$に内分する点$\text{P}$の座標は

\[\large (p_1, p_2)=\left(\frac{mb_1+na_1}{m+n}, y\right)\]

となることがわかります。

2. 線分$\text{AB}$がy軸に平行な場合

　線分$\text{AB}$がy軸に平行な場合、3点$\text{A, B, P}$のx座標は等しくなります。すなわち、$a_1=b_1=p_1$の場合です。ここではx座標を$x$とおきます。
このとき線分$\text{AB}$の長さは2点$\text{A, B}$それぞれのy座標の差分の絶対値で求められるので$|b_2-a_2|$となります。

線分$\text{AP}$の長さは

\[\text{AP}=\frac{m}{m+n}|b_2-a_2|\]

線分$\text{BP}$の長さは

\[\text{BP}=\frac{n}{m+n}|b_2-a_2|\]

と表すことができます。

$a_2<b_2$のとき

　$a_2<b_2$のとき、点$\text{A, B}$の位置関係は上図と同様であり、線分$\text{AB}$の長さは$|b_2-a_2|=b_2-a_2$と表されます。

点$\text{P}$は点$\text{A}$からy軸方向に線分$\text{AP}$の長さの分だけ平行移動した先にあるため、点$\text{P}$のy座標は

\begin{align*}p_2&=a_2+\frac{m}{m+n}|b_2-a_2|\\[0.5em]&=a_2+\frac{m}{m+n}(b_2-a_2)\\[0.5em]&=\frac{(m+n)a_2+m(b_2-a_2)}{m+n}\\[0.5em]&=\frac{mb_2+na_2}{m+n}\end{align*}

すなわち、点$\text{P}$の座標は

\[(p_1, p_2)=\left(x, \frac{mb_2+na_2}{m+n}\right)\]

と表すことができます。

$a_2>b_2$のとき

　$a_2>b_2$のとき、点$\text{A, B}$の位置関係は上図のようになり、線分$\text{AB}$の長さは$|b_2-a_2|=a_2-b_2$と表されます。

点$\text{P}$は点$\text{B}$からy軸方向に線分$\text{BP}$の長さの分だけ平行移動した先にあるため、点$\text{P}$のy座標は

\begin{align*}p_2&=b_2+\frac{n}{m+n}|b_2-a_2|\\[0.5em]&=b_2+\frac{n}{m+n}(a_2-b_2)\\[0.5em]&=\frac{(m+n)b_2+n(a_2-b_2)}{m+n}\\[0.5em]&=\frac{mb_2+na_2}{m+n}\end{align*}

すなわち、点$\text{P}$の座標は

\[(p_1, p_2)=\left(x, \frac{mb_2+na_2}{m+n}\right)\]

と表すことができます。

　以上より、点$\text{A, B}$のy座標の大小関係がどのようであってもy軸に平行な線分$\text{AB}$を$m:n$に内分する点$\text{P}$の座標は

\[\large (p_1, p_2)=\left(x, \frac{mb_2+na_2}{m+n}\right)\]

となることがわかります。

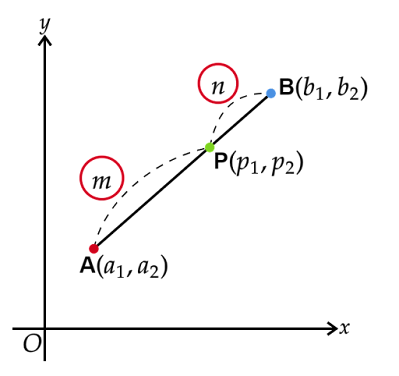
3. 線分$\text{AB}$がx軸にもy軸にも平行でない場合

　線分$\text{AB}$がx軸にもy軸にも平行でない場合、$a_1\neq b_1$かつ$a_2\neq b_2$であり上図のようになります。（ただし、上図は$a_1<b_1$かつ$a_2<b_2$の場合）

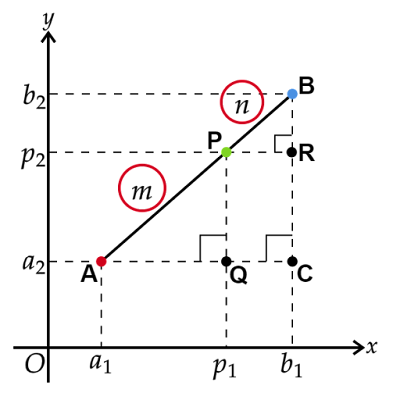
点$\text{A}$を通るx軸に平行な直線$y=a_2$と点$\text{B}$を通るy軸に平行な直線$x=b_1$を引き、その交点を$\text{C}$とします。点$\text{C}$は点$\text{A}$と等しいy座標、点$\text{B}$と等しいx座標をもちます。
また、点$\text{P}$を通るy軸に平行な直線$x=p_1$と$\text{AC}$との交点を$\text{Q}$、点$\text{P}$を通るx軸に平行な直線$y=p_2$と$\text{BC}$との交点を$\text{R}$とします。点$\text{Q}$は点$\text{P}$と等しいx座標、点$\text{R}$は点$\text{P}$と等しいy座標をもちます。

ここで$△\text{APQ}$と$△\text{PBR}$に着目すると

• $\text{PQ}//\text{BR}$より同位角は等しいので$∠\text{APQ}=∠\text{PBR}$
• x軸とy軸は垂直で、それぞれに平行な直線同士も垂直となるから$∠\text{AQP}=∠\text{PRB}=90°$

2組の角がそれぞれ等しいので$△\text{APQ}$と$△\text{PBR}$は相似であることがわかります。

$\text{AP}:\text{BP}=m:n$は相似比となるため、同様に$\text{AQ}:\text{PR}=\text{PQ}:\text{BR}=m:n$。さらに四角形$\text{PQCR}$は長方形なので$\text{PQ}=\text{CR, PR}=\text{CQ}$より

\[\text{AQ}:\text{CQ}=\text{CR}:\text{BR}=m:n \tag{*}\]

が成り立つことがわかります。

これは$a_1, b_1$と$a_2, b_2$の大小関係に関わらず成り立ちます。
$(*)$が成り立つということは点$\text{Q}$は線分$\text{AC}$を$m:n$に内分する点、点$\text{R}$は線分$\text{BC}$を$m:n$に内分する点であるということです。
すると、点$\text{Q}$のx座標と点$\text{R}$のy座標を求めることができれば点$\text{P}$の座標がわかります。

線分$\text{AC}$はx軸に平行な線分でその長さは$|b_1-a_1|$です。
したがって、$1.$より点$\text{Q}$のx座標$p_1$は

\[p_1=\frac{mb_1+na_1}{m+n}\]

と求められます。

線分$\text{BC}$はy軸に平行な線分でその長さは$|b_2-a_2|$です。
したがって、$2.$より点$\text{R}$のy座標$p_2$は

\[p_2=\frac{mb_2+na_2}{m+n}\]

と求められます。

以上より点$\text{P}$の座標は

\begin{equation}(p_1, p_2)=\left(\frac{mb_1+na_1}{m+n}, \frac{mb_2+na_2}{m+n}\right)\end{equation}

と表されることがわかります。

　ここで$(1)$のy座標に$b_2=a_2$を代入すると

\begin{align*}p_2&=\frac{ma_2+na_2}{m+n}\\[0.5em]&=\frac{(m+n)a_2}{m+n}\\[0.5em]&=a_2\end{align*}

すなわち$a_2=b_2=p_2$が成り立って点$\text{P}$の座標が$\left(\frac{mb_1+na_1}{m+n}, a_2\right)$となり、$1.$の場合の点$\text{P}$の座標と一致します。

また、$(1)$のx座標に$b_1=a_1$を代入すると

\begin{align*}p_1\frac{ma_1+na_1}{m+n}\\[0.5em]&=\frac{(m+n)a_1}{m+n}\\[0.5em]&=a_1\end{align*}

すなわち$a_1=b_1=p_1$が成り立って点$\text{P}$の座標が$\left(a_1, \frac{mb_2+na_2}{m+n}\right)$となり、$2.$の場合の点$\text{P}$の座標と一致します。

以上より線分$\text{AB}$がどのような位置にあっても$m:n$に内分する点$\text{P}$の座標は

\[\large\color{red}\text{P}\left(\frac{mb_1+na_1}{m+n}, \frac{mb_2+na_2}{m+n}\right)\]

と表せることがわかります。

　さらに$m=n$のとき点$\text{P}$の座標は

\begin{align*}\left(\frac{mb_1+ma_1}{m+m}, \frac{mb_2+ma_2}{m+m}\right)&=\left(\frac{m(a_1+b_1)}{2m}, \frac{m(a_2+b_2)}{2m}\right)\\[0.5em]&=\left(\frac{a_1+b_1}{2}, \frac{a_2+b_2}{2}\right)\end{align*}

となり、中点の座標と一致します。

関連：座標平面上の分点の座標 ②外分点の座標

関連：座標平面上の線分の中点の座標を求める

関連：内分と外分