座標平面上の分点の座標 ②外分点の座標 ~ 数学について考えてみる

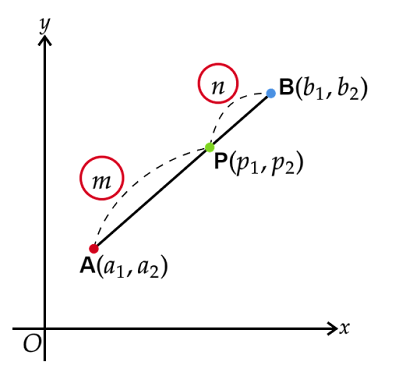
　座標平面の2点

$\text{A}(a_1, a_2), \text{B}(b_1, b_2)$ を結ぶ線分

$\text{AB}$ を

$m:n$ に外分する点

$\text{P}(p_1, p_2)$ の

$p_1, p_2$ はそれぞれ

$a_1, a_2, b_1, b_2$ をもちいてどのように表されるでしょうか？

$m$ と

$n$ の大小関係で場合分けします。

1. $m>n$ のとき

$m>n$ のとき、外分点

$\text{P}$ は上図のように線分

$\text{AB}$ の

$\text{B}$ のほうの延長上にあります。

1-1. 線分 $\text{AB}$ がx軸に平行な場合

　線分

$\text{AB}$ がy軸に平行な場合、3点

$\text{A, B, P}$ のy座標は等しくなります。すなわち、

$a_2=b_2=p_2$ の場合です。ここではy座標を

$y$ とおきます。

このとき線分

$\text{AB}$ の長さは線分の両端の2点

$\text{A, B}$ それぞれのy座標の差分の絶対値で求められるので

$|b_1-a_1|$ となります。

線分

$\text{AP}$ の長さは

$\text{AP}=\frac{m}{m-n}|b_1-a_1|$

線分

$\text{BP}$ の長さは

$\text{BP}=\frac{n}{m-n}|b_1-a_1|$

と表すことができます。

$a_1<b_1$ のとき

$a_1<b_1$ のとき、点

$\text{A, B}$ の位置関係は上図と同様であり、線分

$\text{AB}$ の長さは

$|b_1-a_1|=b_1-a_1$ と表されます。

点

$\text{P}$ は点

$\text{A}$ からx軸の正の方向に線分

$\text{AP}$ の長さの分だけ平行移動した先にあるため、点

$\text{P}$ のx座標は

$\begin{align*}p_1&=a_1+\frac{m}{m-n}|b_1-a_1|\\[0.5em]&=a_1+\frac{m}{m-n}(b_1-a_1)\\[0.5em]&=\frac{(m-n)a_1+m(b_1-a_1)}{m-n}\\[0.5em]&=\frac{mb_1-na_1}{m-n}\end{align*}$

すなわち、点

$\text{P}$ の座標は

$(p_1, p_2)=\left(\frac{mb_1-na_1}{m-n}, y\right)$

と表すことができます。

$a_1>b_1$ のとき

$a_1>b_1$ のとき、点

$\text{A, B}$ の位置関係は上図のようになり、線分

$\text{AB}$ の長さは

$|b_1-a_1|=a_1-b_1$ と表されます。

点

$\text{P}$ は点

$\text{B}$ からx軸の負の方向に線分

$\text{BP}$ の長さの分だけ平行移動した先にあるため、点

$\text{P}$ のx座標は

$\begin{align*}p_1&=b_1-\frac{n}{m-n}|b_1-a_1|\\[0.5em]&=b_1-\frac{n}{m-n}(a_1-b_1)\\[0.5em]&=\frac{(m-n)b_1-n(a_1-b_1)}{m-n}\\[0.5em]&=\frac{mb_1-na_1}{m-n}\end{align*}$

すなわち、点

$\text{P}$ の座標は

$(p_1, p_2)=\left(\frac{mb_1-na_1}{m-n}, y\right)$

と表すことができます。

　以上より、点

$\text{A, B}$ のx座標の大小関係がどのようであってもx軸に平行な線分

$\text{AB}$ を

$m:n$ （ただし、

$m>n$ ）に外分する点

$\text{P}$ の座標は

$\large (p_1, p_2)=\left(\frac{mb_1-na_1}{m-n}, y\right)$

となることがわかります。

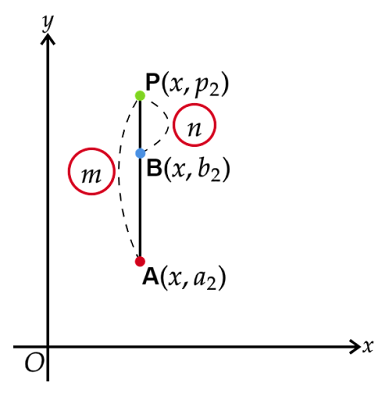
1-2. 線分 $\text{AB}$ がy軸に平行な場合

　線分

$\text{AB}$ がy軸に平行な場合、3点

$\text{A, B, P}$ のx座標は等しくなります。すなわち、

$a_1=b_1=p_1$ の場合です。ここではx座標を

$x$ とおきます。

このとき線分

$\text{AB}$ の長さは2点

$\text{A, B}$ それぞれのy座標の差分の絶対値で求められるので

$|b_2-a_2|$ となります。

線分

$\text{AP}$ の長さは

$\text{AP}=\frac{m}{m-n}|b_2-a_2|$

線分

$\text{BP}$ の長さは

$\text{BP}=\frac{n}{m-n}|b_2-a_2|$

と表すことができます。

$a_2<b_2$ のとき

$a_2<b_2$ のとき、点

$\text{A, B}$ の位置関係は上図と同様であり、線分

$\text{AB}$ の長さは

$|b_2-a_2|=b_2-a_2$ と表されます。

点

$\text{P}$ は点

$\text{A}$ からy軸の正の方向に線分

$\text{AP}$ の長さの分だけ平行移動した先にあるため、点

$\text{P}$ のy座標は

$\begin{align*}p_2&=a_2+\frac{m}{m-n}|b_2-a_2|\\[0.5em]&=a_2+\frac{m}{m-n}(b_2-a_2)\\[0.5em]&=\frac{(m-n)a_2+m(b_2-a_2)}{m-n}\\[0.5em]&=\frac{mb_2-na_2}{m-n}\end{align*}$

すなわち、点

$\text{P}$ の座標は

$(p_1, p_2)=\left(x, \frac{mb_2-na_2}{m-n}\right)$

と表すことができます。

$a_2>b_2$ のとき

$a_2>b_2$ のとき、点

$\text{A, B}$ の位置関係は上図のようになり、線分

$\text{AB}$ の長さは

$|b_2-a_2|=a_2-b_2$ と表されます。

点

$\text{P}$ は点

$\text{B}$ からy軸の負の方向に線分

$\text{BP}$ の長さの分だけ平行移動した先にあるため、点

$\text{P}$ のy座標は

$\begin{align*}p_2&=b_2-\frac{n}{m-n}|b_2-a_2|\\[0.5em]&=b_2-\frac{n}{m-n}(a_2-b_2)\\[0.5em]&=\frac{(m-n)b_2-n(a_2-b_2)}{m-n}\\[0.5em]&=\frac{mb_2-na_2}{m-n}\end{align*}$

すなわち、点

$\text{P}$ の座標は

$(p_1, p_2)=\left(x, \frac{mb_2-na_2}{m-n}\right)$

と表すことができます。

　以上より、点

$\text{A, B}$ のy座標の大小関係がどのようであってもy軸に平行な線分

$\text{AB}$ を

$m:n$ （ただし、

$m>n$ ）に外分する点

$\text{P}$ の座標は

$\large (p_1, p_2)=\left(x, \frac{mb_2-na_2}{m-n}\right)$

となることがわかります。

1-3. 線分 $\text{AB}$ がx軸にもy軸にも平行でない場合

　線分

$\text{AB}$ がx軸にもy軸にも平行でない場合、

$a_1\neq b_1$ かつ

$a_2\neq b_2$ であり上図のようになります。（ただし、上図は

$a_1<b_1$ かつ

$a_2<b_2$ の場合）

点

$\text{A}$ を通るx軸に平行な直線

$y=a_2$ と点

$\text{B}$ を通るy軸に平行な直線

$x=b_1$ を引き、その交点を

$\text{C}$ とします。点

$\text{C}$ は点

$\text{A}$ と等しいy座標、点

$\text{B}$ と等しいx座標をもちます。
また、点

$\text{P}$ を通るy軸に平行な直線

$x=p_1$ と

$\text{AC}$ との交点を

$\text{Q}$ 、点

$\text{P}$ を通るx軸に平行な直線

$y=p_2$ と

$\text{BC}$ との交点を

$\text{R}$ とします。点

$\text{Q}$ は点

$\text{P}$ と等しいx座標、点

$\text{R}$ は点

$\text{P}$ と等しいy座標をもちます。

ここで

$△\text{APQ}$ と

$△\text{PBR}$ に着目すると

$\text{PQ}//\text{BR}$ より錯角は等しいので $∠\text{APQ}=∠\text{PBR}$
x軸とy軸は垂直で、それぞれに平行な直線同士も垂直となるから $∠\text{AQP}=∠\text{PRB}=90°$

2組の角がそれぞれ等しいので

$△\text{APQ}$ と

$△\text{PBR}$ は相似であることがわかります。

$\text{AP}:\text{BP}=m:n$ は相似比となるため、同様に

$\text{AQ}:\text{PR}=\text{PQ}:\text{BR}=m:n$ 。さらに四角形

$\text{PQCR}$ は長方形なので

$\text{PQ}=\text{CR, PR}=\text{CQ}$ より

$\text{AQ}:\text{CQ}=\text{CR}:\text{BR}=m:n \tag{*}$

が成り立つことがわかります。

これは

$a_1, b_1$ と

$a_2, b_2$ の大小関係に関わらず成り立ちます。

$(*)$ が成り立つということは点

$\text{Q}$ は線分

$\text{AC}$ を

$m:n$ に外分する点、点

$\text{R}$ は線分

$\text{BC}$ を

$m:n$ に外分する点であるということです。
すると、点

$\text{Q}$ のx座標と点

$\text{R}$ のy座標を求めることができれば点

$\text{P}$ の座標がわかります。

線分

$\text{AC}$ はx軸に平行な線分でその長さは

$|b_1-a_1|$ です。<> したがって、

$1.$ より点

$\text{Q}$ のx座標

$p_1$ は

$p_1=\frac{mb_1-na_1}{m-n}$

と求められます。

線分

$\text{BC}$ はy軸に平行な線分でその長さは

$|b_2-a_2|$ です。
したがって、

$2.$ より点

$\text{R}$ のy座標

$p_2$ は

$p_2=\frac{mb_2-na_2}{m-n}$

と求められます。

以上より点

$\text{P}$ の座標は

$\begin{equation}(p_1, p_2)=\left(\frac{mb_1-na_1}{m-n}, \frac{mb_2-na_2}{m-n}\right)\end{equation}$

と表されることがわかります。

　ここで

$(1)$ のy座標に

$b_2=a_2$ を代入すると

$\begin{align*}p_2&=\frac{ma_2-na_2}{m-n}\\[0.5em]&=\frac{(m-n)a_2}{m-n}\\[0.5em]&=a_2\end{align*}$

すなわち

$a_2=b_2=p_2$ が成り立って点

$\text{P}$ の座標が

$\left(\frac{mb_1-na_1}{m-n}, a_2\right)$ となり、

$1.$ の場合の点

$\text{P}$ の座標と一致します。

また、

$(1)$ のx座標に

$b_1=a_1$ を代入すると

$\begin{align*}p_1\frac{ma_1-na_1}{m-n}\\[0.5em]&=\frac{(m-n)a_1}{m-n}\\[0.5em]&=a_1\end{align*}$

すなわち

$a_1=b_1=p_1$ が成り立って点

$\text{P}$ の座標が

$\left(a_1, \frac{mb_2-na_2}{m-n}\right)$ となり、

$2.$ の場合の点

$\text{P}$ の座標と一致します。

以上より線分

$\text{AB}$ がどのような位置にあっても

$m:n$ （ただし、

$m>n$ ）に外分する点

$\text{P}$ の座標は

$\begin{equation}\large \text{P}\left(\frac{mb_1-na_1}{m-n}, \frac{mb_2-na_2}{m-n}\right)\end{equation}$

と表せることがわかります。

2. $m<n$ のとき

$m<n$ のとき、外分点

$\text{P}$ は上図のように線分

$\text{AB}$ の

$\text{A}$ のほうの延長上にあります。
このときの点

$\text{P}$ の座標も

$1.$ と同様の手順で求めることができますが、

$1.$ の場合の外分点

$\text{P}$ の座標を利用して

$2.$ の場合の外分点

$\text{P}$ の座標を求めてみます。

$2.$ の場合を「線分

$\text{BA}$ を

$n:m$ （ただし

$n>m$ ）に外分する点

$\text{P}$ 」と考えると、

$1.$ の場合を「線分

$\text{AB}$ を

$m:n$ （ただし

$m>n$ ）に外分する点

$\text{P}$ 」と比較して点

$\text{A}$ と点

$\text{B}$ 、

$m$ と

$n$ を入れ替えただけのものであることがわかります。

したがって、

$(2)$ の2点

$\text{A, B}$ のx座標

$a_1$ と

$b_1$ 、y座標

$a_2$ と

$b_2$ 、比の

$m$ と

$n$ を入れ替えると

$2.$ の場合の外分点

$\text{P}$ の座標となります。

$\begin{align*}(p_1, p_2)&=\left(\frac{na_1-mb_1}{n-m}, \frac{na_2-mb_2}{n-m}\right)\\[0.5em]&=\left(\frac{na_1-mb_1}{n-m}\cdot\frac{-1}{-1}, \frac{na_2-mb_2}{n-m}\cdot\frac{-1}{-1}\right)\\[0.5em]&=\left(\frac{mb_1-na_1}{m-n}, \frac{mb_2-na_2}{m-n}\right)\end{align*}$

となり、結局は

$(2)$ と一致します。

すなわち

$m$ と

$n$ の大小関係がどのようであっても線分

$\text{AB}$ を

$m:n$ に外分する点

$\text{P}$ の座標は

$\large\color{red}\text{P}\left(\frac{mb_1-na_1}{m-n}, \frac{mb_2-na_2}{m-n}\right)$

と表せることがわかります。

　内分点の座標と外分点の座標では少し式の形が異なりますが、線分

$\text{AB}$ が分点

$\text{P}$ によって2つの線分

$\text{AP, BP}$ のうち端点を除いて完全に線分

$\text{AB}$ の外部にある線分に対応する比の数の正負を反転することにすれば、内分点

$\text{P}$ の座標

$\large\color{blue}\text{P}\left(\frac{mb_1+na_1}{m+n}, \frac{mb_2+na_2}{m+n}\right)$

を内分・外分問わずに利用することができます。

線分 $\text{AB}$ を $m:n$ に内分する点 $\text{P}$ の座標

　そのまま利用します。

$\large \text{P}\left(\frac{mb_1+na_1}{m+n}, \frac{mb_2+na_2}{m+n}\right)$

線分 $\text{AB}$ を $m:n$ （ただし $m>n$ ）に外分する点 $\text{P}$ の座標

　端点を除き完全に線分

$\text{AB}$ の外部にある線分は線分

$\text{BP}$ なので、これに対応する

$n$ を

$-n$ に置き換えます。

$\begin{align*}\text{P}\left(\frac{mb_1+(-n)a_1}{m+(-n)}, \frac{mb_2+(-n)a_2}{m+(-n)}\right)&=\large{\left(\frac{mb_1-na_1}{m-n}, \frac{mb_2-na_2}{m-n}\right)}\end{align*}$

すると外分点の座標を表す式と一致します。

線分 $\text{AB}$ を $m:n$ （ただし $m<n$ ）に外分する点 $\text{P}$ の座標

　端点を除き完全に線分

$\text{AB}$ の外部にある線分は線分

$\text{AP}$ なので、これに対応する

$m$ を

$-m$ に置き換えます。

$\begin{align*}\text{P}\left(\frac{(-m)b_1+na_1}{(-m)+n}, \frac{(-m)b_2+na_2}{(-m)+n}\right)&=\left(\frac{-mb_1+na_1}{-m+n}, \frac{-mb_2+na_2}{-m+n}\right)\\[0.5em]&=\left(\frac{na_1-mb_1}{n-m}\cdot\frac{-1}{-1}, \frac{na_2-mb_2}{n-m}\cdot\frac{-1}{-1}\right)\\[0.5em]&=\large{\left(\frac{mb_1-na_1}{m-n}, \frac{mb_2-na_2}{m-n}\right)}\end{align*}$

すると外分点の座標を表す式と一致します。