円に内接する四角形の面積は？（余弦定理・トレミーの定理）

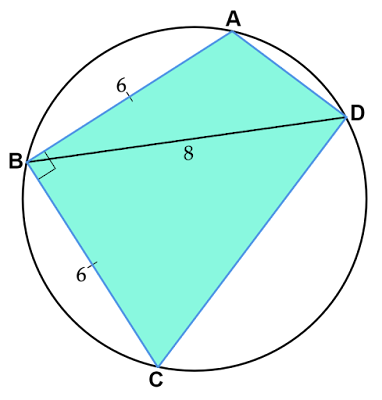
「$\text{AB}=\text{BC}=6,$ $\text{BD}=8,$ $∠\text{ABC}=90°$である円に内接する四角形$\text{ABCD}$がある。四角形$\text{ABCD}$の面積を求めよ。」

　問題の条件に沿うような四角形$\text{ABCD}$を考えてみると上図のようになります。この四角形$\text{ABCD}$の面積を2通りの方法で求めてみます。

1. 余弦定理を利用する方法

　四角形$\text{ABCD}$の対角線$\text{AC}$を引くと、$\text{AB}=\text{BC}=6,$ $∠\text{ABC}=90°$である直角二等辺三角形$\text{ABC}$ができます。したがって、$∠\text{ACB}=∠\text{BAC}=45°$です。

また、円周角の定理より$∠\text{ACB}=∠\text{ADB},$ $∠\text{BAC}=∠\text{BDC}$なので、$∠\text{ADB}=∠\text{BDC}=45°$であることがわかります。

　$△\text{ABD}$と$△\text{BCD}$に着目すると、長さが$6,8$の辺をもち、長さ$6$の辺の対角が$45°$であることが共通しています。

ところで、長さが$a,b$の辺をもち、長さ$a$の辺の対角が$θ$である三角形は最大で2個存在します。できる三角形が直角三角形でない場合、上図のように残る1辺の長さには2通りの可能性があるためです。
この2通りの辺の長さは$a,b,θ$をもちいて余弦定理より求めたとき、2次方程式の異なる正の解として現れます。

そこで長さが$6,8$の辺をもち、長さ$6$の辺の対角が$45°$である三角形の残る1辺の長さを$x$として余弦定理から求めると

$$\begin{align*}6^2&=x^2+8^2-2\cdot8x\cdot\cos45°\\[0.5em]36&=x^2+64-16x\cdot\frac{\sqrt{2}}{2}\\[0.5em]x^2-8\sqrt{2}x+28&=0\\[0.5em]x&=4\sqrt{2}\pm\sqrt{\bigl(-4\sqrt{2}\bigr)^2-28}\\[0.5em]&=4\sqrt{2}\pm2\end{align*}$$

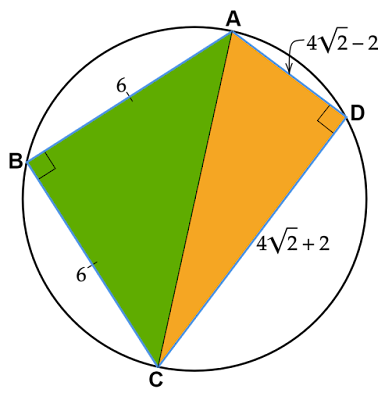
となり、これらが$△\text{ABD},△\text{BCD}$それぞれにある長さ不明の辺$\text{AD, CD}$の長さとなります。問題の図の場合は、短い方の辺$\text{AD}$の長さが$4\sqrt{2}-2$、長い方の辺$\text{CD}$の長さが$4\sqrt{2}+2$となります。

関連：余弦定理　なぜ成り立つ？

（問題の図では$\text{AD}<\text{CD}$としていますが、上図のように$\text{AD}>\text{CD}$でも問題の条件を満たします。すなわち$\text{AD}=4\sqrt{2}+2,\text{CD}=4\sqrt{2}-2$の場合もあります。）

　四角形$\text{ABCD}$の面積は$△\text{ABC}$と$△\text{ACD}$の面積の和でもあります。

$△\text{ABC},△\text{ACD}$はともに直角三角形なので

$$\begin{align*}△\text{ABC}&=\frac{1}{2}\text{AB}\cdot \text{BC}\\[0.5em]&=\frac{1}{2}\cdot6^2\\[0.5em]&=18\\[1em]△ \text{ACD}&=\frac{1}{2}\text{AD}\cdot \text{CD}\\[0.5em]&=\frac{1}{2}(4\sqrt{2}-2)(4\sqrt{2}+2)\\[0.5em]&=14\end{align*}$$
したがって、四角形$\text{ABCD}$の面積は
$$\begin{align*}□ \text{ABCD}&=△\text{ABC}+△ \text{ACD}\\[0.5em]&=18+14\\[0.5em]&=32\end{align*}$$

と求められます。

もちろんブラーマグプタの公式から求めることもできます。

$$\begin{align*}s&=\frac{\text{AB}+\text{BC}+\text{CD}+\text{AD}}{2}\\[0.5em]&=\frac{6+6+(4\sqrt{2}+2)+(4\sqrt{2}-2)}{2}\\[0.5em]&=6+4\sqrt{2}\\[1em]□ \text{ABCD}&=\sqrt{(s-\text{AB})(s-\text{BC})(s-\text{CD})(s-\text{AD})}\\[0.5em]&=\sqrt{4\sqrt{2}\cdot4\sqrt{2}\cdot8\cdot4}\\[0.5em]&=32\end{align*}$$

関連：円に内接する四角形の面積を求める方法 ブラーマグプタの公式

2. トレミーの定理を利用する方法

　四角形$\text{ABCD}$の面積を$△\text{ABC}$と$△\text{ACD}$の面積の和から求めるのは$1.$と共通ですが、$△\text{ACD}$の面積をトレミーの定理を利用して求めます。

関連：加法定理と正弦定理でトレミーの定理を証明してみる

　四角形$\text{ABCD}$の対角線$\text{AC}$を引くと、$\text{AB}=\text{BC}=6,$ $∠\text{ABC}=90°$である直角二等辺三角形$\text{ABC}$ができます。
すると、タレスの定理の逆より辺$\text{AC}$は直角三角形$\text{ABC}$の外接円の直径であることがわかります。これはすなわち四角形$\text{ABCD}$の外接円の直径であるということです。
その長さは直角二等辺三角形の3辺の比より$\text{AC}=6\sqrt{2}$であることがわかります。
さらにタレスの定理より$∠\text{ADC}$は直径$\text{AC}$の円周角なので$∠\text{ADC}=90°$であり、$△\text{ACD}$が直角三角形であることがわかります。

関連：タレスの定理とその逆

ゆえに$△\text{ACD}$において三平方の定理

$$\begin{align*}\text{AC}^2&=\text{AD}^2+\text{CD}^2\\[0.5em]\text{AD}^2+\text{CD}^2&=72\tag1\end{align*}$$

が成り立ち、面積が

$$△\text{ACD}=\frac{1}{2}\text{AD}\cdot\text{CD}\tag2$$

で求められます。

トレミーの定理より

$$\begin{align*}\text{AB}\cdot\text{CD}+\text{AD}\cdot\text{BC}&=\text{AC}\cdot \text{BD}\\[0.5em]6\text{CD}+6\text{AD}&=6\sqrt{2}\cdot8\\[0.5em]\text{AD}+\text{CD}&=8\sqrt{2}\end{align*}$$

これの両辺を2乗すると

$$\begin{align*}(\text{AD}+\text{CD})^2&=\bigl(8\sqrt{2}\bigr)^2\\[0.5em]\text{AD}^2+2\text{AD}\cdot \text{CD}+\text{CD}^2&=128\\[0.5em]\bigl(\text{AD}^2+\text{CD}^2\bigr)+2\cdot2\left(\frac{1}{2}\text{AD}\cdot \text{CD}\right)&=128\end{align*}$$

$(1),(2)$より

$$\begin{align*}72+2\cdot2△\text{ACD}&=128\\[0.5em]4△ \text{ACD}&=56\\[0.5em]△\text{ACD}&=14\end{align*}$$

と求められます。

　$△\text{ABC}$の面積は

$$\begin{align*}△\text{ABC}&=\frac{1}{2}\text{AB}\cdot \text{BC}\\[0.5em]&=\frac{1}{2}\cdot6^2\\[0.5em]&=18\end{align*}$$

なので、四角形$\text{ABCD}$の面積は

$$\begin{align*}□\text{ABCD}&=△\text{ABC}+△ \text{ACD}\\[0.5em]&=18+14\\[0.5em]&=32\end{align*}$$

であることがわかります。