球を平面で2つの立体に切断して、そのうちの1つの立体の体積が球の体積の$\dfrac{1}{4}$となるとき、切断する平面は球の中心からどのくらい離れた位置にあるでしょうか？
これを求めるには回転体の体積を利用します。
.png)
これのグラフとx軸で囲まれた部分をx軸を回転軸として1回転させてできるのが中心が原点で半径$1$の球であり、これの体積は
\[\pi\int^1_{-1}\bigl(\sqrt{1-x^2}\bigr)^2dx=\pi\int^1_{-1}1-x^2dx\]
より求められます。積分区間が$-1\leqq
x\leqq1$なのは、それが$y=\sqrt{1-x^2}$の定義域であるためです。これはこの球が座標空間においてx軸に垂直な$(-1,0)$を含む平面（平面方程式$x=-1$）とx軸に垂直な$(1,0)$を含む平面$x=1$の間に存在するともいえます。
この球の体積を求めてみると
\begin{align*}\pi\int^1_{-1}1-x^2dx&=\pi\left[x-\frac{1}{3}x^3\right]^1_{-1}\\[0.5em]&=\pi\left[\left(1-\frac{1}{3}\right)-\left\{-1-\frac{(-1)^3}{3}\right\}\right]\\[0.5em]&=\pi\left\{\frac{2}{3}-\left(-\frac{2}{3}\right)\right\}\\[0.5em]&=\frac{4}{3}\pi\end{align*}
となります。
.png)
\[\pi\int^t_{-1}1-x^2dx\]
と表すことができます。これが球の$\dfrac{1}{4}$の体積、すなわち$\dfrac{\pi}{3}$となるときの$t$を求めてみます。
条件より
\begin{align*}\pi\int^t_{-1}1-x^2dx&=\frac{\pi}{3}\\[0.5em]\int^t_{-1}1-x^2dx&=\frac{1}{3}\\[0.5em]\left[x-\frac{1}{3}x^3\right]^t_{-1}&=\frac{1}{3}\\[0.5em]\left(t-\frac{1}{3}t^3\right)-\left(-\frac{2}{3}\right)&=\frac{1}{3}\\[0.5em]t-\frac{1}{3}t^3&=-\frac{1}{3}\\[0.5em]3t-t^3&=-1\\[0.5em]t^3-3t-1&=0\end{align*}
この3次方程式を解けば$t$が求まりますが、有理数解がないのでニュートン法をもちいて近似解を求めます。
ニュートン法とは、曲線の接線のx切片を利用して近似解を求める方法です。これを利用するには曲線の方程式とその導関数と接線のx切片を求める式が必要となります。
3次方程式$t^3-3t-1=0$を解く際にもちいる曲線の方程式は$y=f(x)=x^3-3x-1$で、これの導関数は$f'(x)=3x^2-3$です。
$x=x_n$における曲線の接線の方程式は$y=f'(x_n)\bigl(x-x_n\bigr)+f(x_n)$で、これのx切片、すなわちx軸との交点$(x_{n+1},0)$の$x_{n+1}$を求める式は
$-1<t<1$より求めたい解の存在範囲も$-1<x<1$となります。$x=0$付近を調べるため最初の接点のx座標$x_0$を$0$とします。
$x=x_n$における曲線の接線の方程式は$y=f'(x_n)\bigl(x-x_n\bigr)+f(x_n)$で、これのx切片、すなわちx軸との交点$(x_{n+1},0)$の$x_{n+1}$を求める式は
\begin{align*}0&=f'(x_n)\bigl(x_{n+1}-x_n\bigr)+f(x_n)\\[0.5em]&=x_{n+1}f'(x_n)-x_nf'(x_n)+f(x_n)\\[0.5em]x_{n+1}f'(x_n)&=x_nf'(x_n)-f(x_n)\\[0.5em]x_{n+1}&=x_n-\frac{f(x_n)}{f'(x_n)}\end{align*}
となります。右辺を$x_n$だけをもちいて表した場合は
\begin{align*}x_{n+1}&=x_n-\frac{{x_n}^3-3x_n-1}{3{x_n}^2-3}\\[0.5em]&=\frac{(3{x_n}^3-3x_n)-({x_n}^3-3x_n-1)}{3{x_n}^2-3}\\[0.5em]\therefore
x_{n+1}&=\frac{2{x_n}^3+1}{3{x_n}^2-3}\end{align*}
となります。$-1<t<1$より求めたい解の存在範囲も$-1<x<1$となります。$x=0$付近を調べるため最初の接点のx座標$x_0$を$0$とします。
これらをもちいて表計算ソフトで計算します。
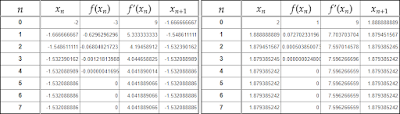
セルへの入力例は下図のようになります。（残りのセルは上のセルからオートフィル機能で埋めます。）
計算結果は下図となります。
$x_{n+1}$の収束値$-0.3472963553$が3次方程式$t^3-3t-1=0$の近似解の1つです。これは解の存在範囲$-1<t<1$も満たしています。
セルへの入力例は下図のようになります。（残りのセルは上のセルからオートフィル機能で埋めます。）
他に実数解がないか求めてみます。（以降、$-0.3472963553$を3次方程式$t^3-3t-1=0$の真の解として扱います。）
他の2解をそれぞれ$α,β$（ただし、$α<β$）とすると、3次方程式の係数と解の関係より
これらは解の存在範囲$-1<t<1$の外にあるので、球を切断する平面$x=t$として適しません。
他の2解をそれぞれ$α,β$（ただし、$α<β$）とすると、3次方程式の係数と解の関係より
\begin{align*}-0.3472963553+\alpha+\beta&=0\tag1\\[0.5em]-0.3472963553\alpha\beta&=1\tag2\end{align*}
$(1)$より
\[\beta=0.3472963553-\alpha\tag3\]
これを$(2)$に代入して
\begin{align*}-0.3472963553\alpha(0.3472963553-\alpha)&=1\\[0.5em]-(0.3472963553)^2\alpha+0.3472963553\alpha^2&=1\\[0.5em]0.3472963553\alpha^2-(0.3472963553)^2\alpha-1=0\\[0.5em]\alpha^2-0.3472963553\alpha-\frac{1}{0.3472963553}&=0\end{align*}
となるので、解の公式より
\begin{align*}\alpha&=\frac{0.3472963553\pm\sqrt{(-0.3472963553)^2-4\left(-\frac{1}{0.3472963553}\right)}}{2}\\[0.5em]&≒-1.532088886,1.879385242\end{align*}
$(3)$と$α<β$であることより
\[\alpha≒-1.532088886,\beta≒1.879385242\]
と求められます。これらはニュートン法でも求めることができます。
以上より、中心が原点で半径$1$の球から球の$\dfrac{1}{4}$の体積を切り取る平面は$x=-0.3472963553$であり、球の中心からの距離は$0.3472963553$であることがわかります。
また、球を平面$x=-0.3472963553$で切断したときの断面の円の直径$d$は、円$x^2+y^2=1$の$x=-0.3472963553$における2点間の距離に等しいので、
また、球を平面$x=-0.3472963553$で切断したときの断面の円の直径$d$は、円$x^2+y^2=1$の$x=-0.3472963553$における2点間の距離に等しいので、
\begin{align*}(-0.3472963553)^2+y^2&=1\\[0.5em]y^2&=1-(-0.3472963553)^2\\[0.5em]y&=\pm\sqrt{1-(-0.3472963553)^2}\end{align*}
より
\begin{align*}d&=\sqrt{1-(-0.3472963553)^2}-\bigl(-\sqrt{1-(-0.3472963553)^2}\bigr)\\[0.5em]&=2\sqrt{1-(-0.3472963553)^2}\\[0.5em]&≒1.875510855\end{align*}
と求められます。
これらを図示したものが以下のものとなります。
外部リンク：ニュートン法 - Wikipedia
Share:
