なぜこのように表すことができるのでしょうか?
2021年12月29日
点と直線の距離はどうやって求める?
2021年12月25日
1次関数が互いに直交する条件は?
2021年12月21日
立方根を含む分数の分母の有理化
直線の方程式と定義域
ただし、$\text{(a)}$は点$\text{A, B}$を含む、$\text{(b)}$は点$\text{B}$を含まないが点$\text{C}$を含む、$\text{(c)}$は点$\text{C}$も$\text{D}$も含まないものとする。」
このような問題はどのように解けばよいでしょうか?
2021年12月16日
多項式を割る式で割ったときの余りと余りを同じ割る式で割ったときの余りが等しいのはなぜ?
これは、なぜ成立するのでしょうか?
括弧の前にマイナスが付いているときは?
分数を含む文字式の計算(足し算・引き算)
2021年12月12日
分数がある1次方程式を解く
2021年12月10日
sin3°、cos3°、tan3°はどんな数?
2021年12月9日
2021年12月5日
円に内接・外接する正多角形の面積を求める公式を作ってみよう
円に内接・外接する正多角形の面積を求めるための式を作ってみようと思います。
2021年12月4日
碁盤の目状の道路網の最短経路は何通り?(2)
2021年12月2日
碁盤の目状の道路網の最短経路は何通り?
2021年11月30日
中線と垂直二等分線の違い
 |
| 図1 中線 |
中線とは、三角形の頂点とその対辺の中点を結ぶ線のことです。
辺を2等分するため二等分線ではありますが、三角形の頂点を通ることも条件なので中線は三角形に関係する二等分線であると言えます。
 |
| 図2 垂直二等分線 |
垂直二等分線とは、線分を二等分し、かつその線分に対し垂直な線のことです。
垂直+二等分線であるので、垂線と二等分線の両方の性質を持つ線です。
中線と異なり必ずしも三角形の頂点を通る必要はないので、三角形だけでなくあらゆる図形に使うことができます。
 |
| 図3 二等辺三角形の中線 |
中線であり、かつ垂直二等分線であるのは二等辺三角形の中線です。頂角と底辺の中点を結ぶ中線は垂直二等分線となります。
特に正三角形の場合は、3本すべての中線が垂直二等分線になります。
2021年11月27日
sin6°、cos6°、tan6°はどんな数?
2021年11月26日
モンティ・ホール問題の全事象の確率を調べてみる
2021年11月25日
-1、i、-iの立方根は?
2021年11月21日
円に内接・外接する正十二角形の周の長さと円周率の関係
2021年11月19日
比の問題の解き方
1. 「AとBは同じテストを受けた。Aのテストの得点は50点、Bの得点は75点だった。
AとBのテストの得点の比を答えよ。」
2. 「AとBは同じテストを受けた。AとBのテストの得点の比は5:4だった。
Aの得点が80点であるとき、Bの得点は何点か?」
2021年11月17日
する数 される数 どっち?
2021年11月13日
複利運用の平均年利の算出
「複利運用でとある金融商品に200万円を投資した。3年後収益率を調べてみると33.1%であった。この金融商品の平均年率は何%であったのかを求めよ。」
どうやって年率を計算すればよいでしょうか?
2021年11月10日
割り算を引き算で表す とは?
2021年11月7日
正三角形の作図法
2021年10月31日
正五角形の作図法
ひし形の対角線が互いの垂直二等分線であることの証明
2021年10月30日
角の二等分線の作図法
角の二等分線は以下のように定規とコンパスを使って作図します。
垂直二等分線の作図法
垂直二等分線の定規とコンパスを使っての作図は以下のようになります。
2021年10月29日
負の分数のマイナスは分母と分子どっちについているの?
$-\dfrac{a}{b}$という負の分数についているマイナスは、分母と分子のどちらについているものと考えればよいのでしょうか?
同じ半径の2円の中心が互いの円周上にあるときにできるおうぎ形の中心角は?
2021年10月27日
円に外接する正六角形の作図法
円に外接する正六角形の定規とコンパスを使っての作図法を2通り紹介します。
2021年10月24日
楽天ポイント利息の年利を計算してみる(単利と複利)
楽天ポイント利息という楽天ポイントを預けておくだけで安定してポイントが増えていくサービスがあります。月利は0.009%とありますが、年利は0.1%以上と具体的には書かれていません。なので、年利で考えたとき具体的にどのくらいになるのかを計算してみます。
円や半円が入った正方形を使った問題
円や扇形を並べた正方形の1辺の長さは?
2021年10月21日
2021年10月18日
sin15°、cos15°、tan15°はどんな数?
2021年10月17日
正六角形がおさまっている正方形の1辺の長さは?
sin12°、cos12°、tan12°はどんな数?
「$\sin18°,\cos18°,\tan18°$はどんな数?」で$18°$における三角関数を調べたので、これを利用して$12°\ (=\dfrac{\pi}{15})$における三角関数を調べてみます。
2021年10月16日
sin18°、cos18°、tan18°はどんな数?
「$\sin72°,\cos72°,\tan72°$はどんな数?」で$72°$のときの三角関数について調べたので、それを利用して$18°\ (=\dfrac{\pi}{10})$のときの三角関数について調べてみます。
2021年10月15日
対頂角、同位角、錯角とは
2021年10月10日
円に内接・外接する正五角形の周の長さと円周率の関係
円に内接・外接する正五角形の周の長さを求めて、円周率との関係を調べてみます。
2021年10月9日
sin72°、cos72°、tan72°はどんな数?
$72°$は$360°$の5分の1なので、5倍角の公式をもちいて$72°\ (=\dfrac{2\pi}{5})$のときの三角関数を求めます。
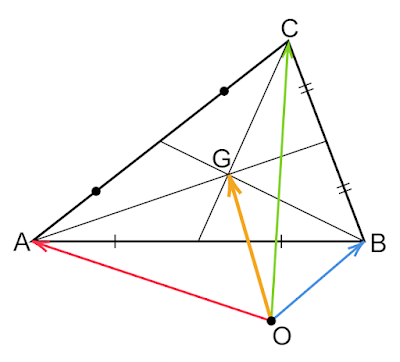
重心の位置ベクトルの求め方 2通り
2021年10月5日
必要条件、十分条件 どっち?
BはAであるための必要条件
AはBであるための十分条件
2021年10月1日
円に内接・外接する正十角形の周の長さと円周率の関係
三角形の重心は中線を何:何に内分する?
「正三角形の重心が中線を2:1に内分するのはなんでだっけ……?」では正三角形だけにしか言及しませんでしたが、あらゆる三角形で重心がどんな性質を持っているかを調べてみます。
2021年9月29日
指数が未知数の方程式 指数方程式
2021年9月27日
相加平均と相乗平均 なぜa=bなのか どっちが最大値?最小値?
2021年9月26日
多項定理を使わずに二項定理で解いてみる
この問題は多項定理を使って解くのですが、二項定理で解いてみます。
2021年9月25日
数の大小比較(平方根の計算・二重根号)
2021年9月22日
2進数を16進数に変換するときなぜ4桁ごとに区切るのか?
2021年9月20日
立方根の方程式
10進数の小数を2進数の小数に変換するには
2021年9月18日
床と2つの円に囲まれた正方形
このような問題はどのように解けばよいでしょうか?
2021年9月16日
2次式の因数分解と平方完成の違い
例として$x^2-6xy+5y^2$という多項式について考えます。
2021年9月15日
円に内接する四角形の対角の和はなぜ180°なのか?
なぜそうなるのかは円周角の定理を利用することでいくつかの方法で確かめることができます。
接線と弦のつくる角(接弦定理)
本当に接弦定理は成り立つのでしょうか?確かめてみます。
10進数を2進数に変換する
10進数
10で1回割ると10より小さい$4$が余りとして出てきます。
商の$123$を10で割ると次は余りとして$3$が出てきます。
2進数
2021年9月11日
2次関数の頂点と1次関数との交点でできる三角形の面積
「2次関数$y=x^2-4x+1$と1次関数$y=-x+5$の交点2点をx座標の小さい方から$\text{A, B}$とし、2次関数の頂点を$\text{P}$とする。このとき、$△\text{ABP}$の面積を求めよ。」
2021年9月10日
順列はなぜ階乗の分数になるのか?
なぜ、順列は階乗の分数で表せるのでしょうか?
2021年9月8日
2次関数のグラフを描く
「関数$y=x^2+2x$のグラフをかけ。」
2021年9月5日
なぜsinを使って三角形の面積が求められるのか?

|
| 図1 三角形\text{ABC} |
なぜこの式で三角形の面積を求めることができるのでしょうか?
aベクトル-bベクトルはなぜこの向きなのか?
2021年9月4日
直交する直線に接する2つの円とその半径

|
| 図1 直交する直線と2つの円 |
「直交する2本の直線を接線とする円が2つあり、円どうしは交わらず接している。小さい方の円の半径が1であるとき、大きい方の円の半径$x$を求めよ。」
このような問題はどのように解けばよいのでしょうか?
2021年9月3日
半径が同じ円が2個入った正方形の1辺の長さは?
2021年9月2日
1つの辺の長さがわかれば面積が求められる特殊な三角形
しかし、三角形の中には1辺の長さが分かれば面積が求められるものが存在します。
それはどんな三角形なのか3つの例を見ていきます。
2021年9月1日
入れ子状態の分数はどうやって簡単にする?
2021年8月31日
どっちが分子でどっちが分母?
割り算、横書きの分数、比の値。そして三角比。それぞれどちらが分子、分母になるのかを見ていきます。
2021年8月28日
鎖の輪のように連なる円の面積の差
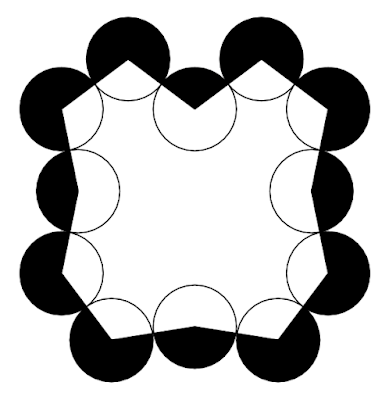 |
| 図1 鎖の輪状に連なる円 |
「図1のように同じ半径の円が鎖の輪のように連なっている。それぞれの円の中心を線でつないでできる図形の内側にある方を白く、外側にある方を黒く円を塗り分けた。円の黒い部分の合計と白い部分の合計の面積の差はいくらになるか。1つの円の面積を1とする。」
三角形の内角・外角の二等分線と線分の比の性質
なぜこれが成り立つのでしょうか?
2021年8月27日
直交する弦の長さから円の半径を求める
2021年8月26日
平方根の計算 分母の有理化
2021年8月25日
平方根の計算 足し算・引き算
2021年8月22日
平行四辺形の中の三角形の面積は?(1つの共通の内角をもつ平行四辺形と三角形の面積)
2021年8月21日
共通の内角を持つ三角形の面積を求める
2021年8月20日
√(-5)^2の答えはなぜ-5じゃなくて5なのか?
$\sqrt{(-5)^2}$(ルート括弧マイナス5の2乗)の答えは$-5$ではなく$5$になります。
ルートと2乗が打ち消し合ったら$-5$じゃん!と考えてしまうかもしれませんが、ちゃんと計算してみると納得します。
2021年8月18日
sin36°がどんな数になるかを求めてみよう
$36°$は$180°$の5分の1なので、「$θ$の5倍角までの$\sin,\cos,\tan$を求めてみよう」で求めた5倍角の式を利用して、$\sin36°\ (=\sin\dfrac{\pi}{5})$がどんな数になるのかを計算してみようと思います。
2021年8月16日
θの5倍角までのsin、cos、tanを求めてみよう
2021年8月15日
円周率は無理数なのに(円周)/(直径)と分数の形で定義されていることが矛盾していないことを正多角形で予測する
2021年8月12日
円に内接・外接する正方形の周の長さを計算してみる
円に内接・外接する正方形の周の長さはどのくらいになるのでしょうか?計算してみました。
円周と正方形の周の長さの関係から円周率の値がどのくらい絞り込めるのかも調べてみました。
2021年8月10日
円に内接・外接する正三角形の周の長さを計算してみる
半径$1$の円に内接・外接する正三角形の周の長さはいくらになるのかを計算してみます。
円周と正三角形の周の長さの関係から円周率の値がどのくらい絞り込めるのかも調べてみます。
2021年8月8日
円に内接・外接する正多角形の周の長さを求める公式を作ってみよう
円に内接・外接する正多角形の周の長さを、円の半径と正多角形の頂点の数から求めることができる式を求めてみようと思います。
2021年8月4日
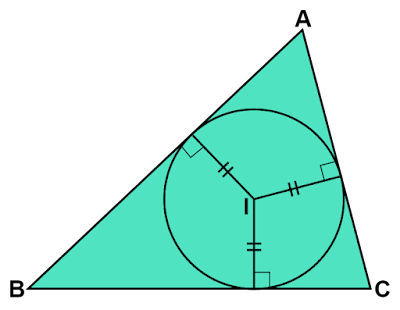
三角形の内心が角の二等分線の交点で求められるのはナゼ?
なぜ、3辺との距離が等しいという性質を利用せずに角の二等分線で作図するのでしょうか?
2021年8月3日
三角形の外心が3辺の垂直二等分線の交点で求められるのはナゼ?
なぜ、頂点からの距離が等しいという性質がありながら垂直二等分線で作図するのでしょうか?

![1/([3]√2+[3]√3)](https://blogger.googleusercontent.com/img/a/AVvXsEhSa0CpLeM099rdiGiqKZOYTlIWtSl02Fjl3k6I44ssyJ49RPEJH0hnEfDgbS6PheL8vsnXMAcfBLesizVs_wrmOxeDYS-lv7B5fAN8oBVSuXYXND-6CRHv56A5yKi2ao-C6DvjTfN5hlYqySaD8iwz3toLeuD4QlkYVssGH6o03Uwjn14Nz4OgThP9=s16000-rw)



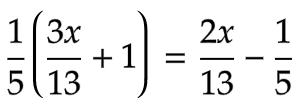












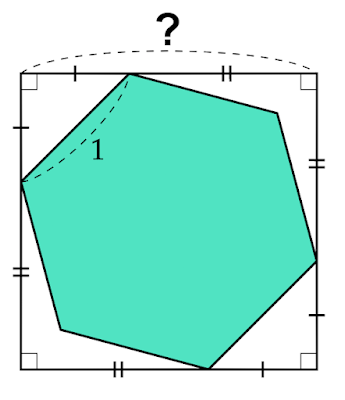

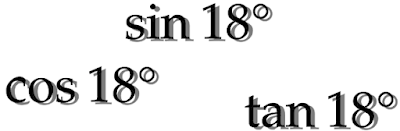









.png)









.png)



