「$504$の正の約数の個数を求めよ。」
約数の数を求めるには素因数分解を利用します。
$504$を素因数分解すると
\[504=2^3×3^2×7\]
となります。
約数とは、ある整数Aを割り切る事ができる整数Bのことで、$504$は$504$の素因数の中からつくった数であれば割り切れるので、これが約数になることがわかります。
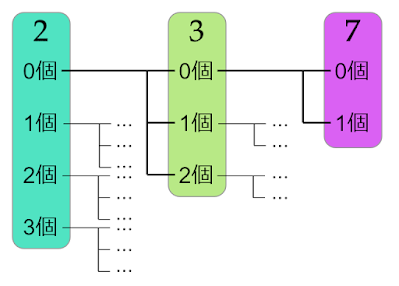
$504$に含まれる素因数は$2$が3個、$3$が2個、$7$が1個です。
最大の約数はこれらの素因数をすべて使った$504$、最小の約数が素因数を1つも使わない$1$で、他の約数は使う素因数の個数を変えた組み合わせで考えることができます。
約数の作り方の選択肢は
であるので、全部で$4×3×2=24$通りあります。
|
| 作れる約数の数は選択肢の数だけ倍加する |
- $2$を使う個数が0個、1個、2個、3個の4通り
- $3$を使う個数が0個、1個、2個の3通り
- $7$を使う個数が0個、1個の2通り
したがって、$504$の正の約数は24個となります。
.png)
また、上図のような樹形図は多項式の展開のときにも見ることができるので、これを利用して$504$の正の約数をすべて挙げるには、素因数を使う個数を指数にして
\[(2^0+2^1+2^2+2^3)(3^0+3^1+3^2)(7^0+7^1)\]
とすれば展開したときの各項がすべて$504$の正の約数になります。
\begin{align*}&(2^0+2^1+2^2+2^3)(3^0+3^1+3^2)(7^0+7^1)\\[0.5em]&=2^0\cdot3^0\cdot7^0+2^0\cdot3^0\cdot7^1+2^0\cdot3^1\cdot7^0\\ &\qquad+2^0\cdot3^1\cdot7^1+2^0\cdot3^2\cdot7^0+2^0\cdot3^2\cdot7^1\\ &\qquad+2^1\cdot3^0\cdot7^0+2^1\cdot3^0\cdot7^1+2^1\cdot3^1\cdot7^0\\ &\qquad+2^1\cdot3^1\cdot7^1+2^1\cdot3^2\cdot7^0+2^1\cdot3^2\cdot7^1\\ &\qquad+2^2\cdot3^0\cdot7^0+2^2\cdot3^0\cdot7^1+2^2\cdot3^1\cdot7^0\\ &\qquad+2^2\cdot3^1\cdot7^1+2^2\cdot3^2\cdot7^0+2^2\cdot3^2\cdot7^1\\ &\qquad+2^3\cdot3^0\cdot7^0+2^3\cdot3^0\cdot7^1+2^3\cdot3^1\cdot7^0\\ &\qquad+2^3\cdot3^1\cdot7^1+2^3\cdot3^2\cdot7^0+2^3\cdot3^2\cdot7^1\\[0.5em]&=1+7+3+21+9+63\\ &\qquad+2+14+6+42+18+126\\ &\qquad+4+28+12+84+36+252\\ &\qquad+8+56+24+168+72+504\end{align*}
となるから、$504$の正の約数を小さい順に並べると
\begin{array}{r}1,&2,&3,&4,&6,&7,\\
8,&9,&12,&14,&18,&21,\\
24,&28,&36,&42,&56,&63,\\
72,&84,&126,&168,&252,&504.\end{array}
であることがわかります。
Share:
