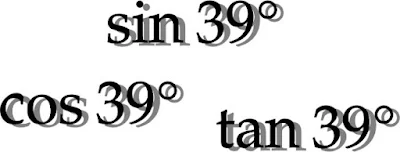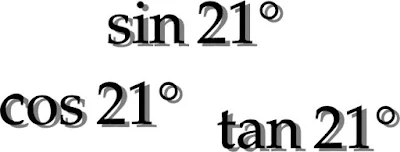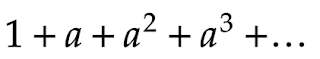このような問題はどのように解けばよいでしょうか?
2022年1月30日
2022年1月29日
2次不等式 mの条件内で常に成り立つxの値の範囲は?
PLUMBAGO関数...2次関数, 式...不等式...2次不等式, 手法...平方完成
「2次不等式$x^2+mx-24<0$の$m$を$2<m<6$の範囲で変化させたとき、2次不等式が常に成り立つ$x$の値の範囲を求めよ。」
Share:
https://p-suugaku.blogspot.com/2022/01/2jifutoushiki-m-x.html2次不等式 mの条件内で常に成り立つxの値の範囲は?
3°刻みで三角関数の式を書く(第四象限 273°~357°編)
PLUMBAGO関数...三角関数.三角比, 量...角度
$3°$刻みで$273°~357°$のときの三角関数がどんな式になるのかをまとめてみました。
Share:
https://p-suugaku.blogspot.com/2022/01/3dokizami-sankakukansuu-4.html3°刻みで三角関数の式を書く(第四象限 273°~357°編)
2022年1月26日
相似な三角形のそれぞれの3辺の比
PLUMBAGO幾何...合同.相似, 幾何...三角形, 数...割合, 数...割合...比
これが成り立つことを確かめます。
Share:
https://p-suugaku.blogspot.com/2022/01/souji-hennohi.html相似な三角形のそれぞれの3辺の比
2022年1月25日
3°刻みで三角関数の式を書く(第三象限 183°~267°編)
PLUMBAGO関数...三角関数.三角比, 量...角度
$3°$刻みで$183°~267°$のときの三角関数がどんな式になるのかをまとめてみました。
Share:
https://p-suugaku.blogspot.com/2022/01/3dokizami-sankakukansuu-3.html3°刻みで三角関数の式を書く(第三象限 183°~267°編)
2022年1月23日
交差したはしごの問題(Crossed ladders problem)の高さの関係
日本語版がないWikipediaの"Crossed ladders problem"にある高さの関係について調べてみました。
Share:
https://p-suugaku.blogspot.com/2022/01/crossed-ladders.html交差したはしごの問題(Crossed ladders problem)の高さの関係
2022年1月22日
三角形の内角の二等分線の長さは?
PLUMBAGO幾何...三角形, 幾何...線...二等分線, 定理...正弦定理.余弦定理, 量...長さ
上図のように$△\text{ABC}$に$∠\text{A}$の二等分線$\text{AP}$を引くと
\[\text{BP}:\text{PC}=\text{AB}:\text{AC}\]
という関係が成り立ちます。
\[\text{BP}:\text{PC}=\text{AB}:\text{AC}\]
という関係が成り立ちます。
ここで$∠\text{A}$の二等分線$\text{AP}$の長さについて考えてみるとどのような関係が見えるのでしょうか?
Share:
https://p-suugaku.blogspot.com/2022/01/kakunonitoubunsen-hi-nagasa.html三角形の内角の二等分線の長さは?
2次関数の最大値・最小値を求める
PLUMBAGO関数...2次関数, 関数...最大値.最小値, 手法...平方完成
1. $y=2x^2+5x-3$
①$-2\leqq x\leqq1$ ②$0\leqq x\leqq3$
2. $y=-x^2+3x+4$
①$-4\leqq x\leqq-1$ ②$1\leqq x\leqq3$」
このような問題はどのように考えればよいでしょうか?
Share:
https://p-suugaku.blogspot.com/2022/01/2jikan.html2次関数の最大値・最小値を求める
2022年1月20日
3°刻みで三角関数の式を書く(第二象限 93°~177°編)
PLUMBAGO関数...三角関数.三角比, 量...角度
$3°$刻みで$93°~177°$のときの三角関数がどんな式になるのかをまとめてみました。
Share:
https://p-suugaku.blogspot.com/2022/01/3dokizami-sankakukansuu-2.html3°刻みで三角関数の式を書く(第二象限 93°~177°編)
sin(23°+111°)をxで表すと?
PLUMBAGO関数...三角関数.三角比
「$\sin23°+\sin67°=x$とするとき、$\sin(23°+111°)$を$x$の式で表せ。」
このような問題はどのように考えればよいでしょうか?
Share:
https://p-suugaku.blogspot.com/2022/01/sin23111x.htmlsin(23°+111°)をxで表すと?
2022年1月17日
3°刻みで三角関数の式を書く(第一象限 3°~87°編)
PLUMBAGO関数...三角関数.三角比, 量...角度
$3°$刻みで$3°~87°$のときの三角関数がどんな式になるのかをまとめてみました。
Share:
https://p-suugaku.blogspot.com/2022/01/3dokizami-sankakukansuu.html3°刻みで三角関数の式を書く(第一象限 3°~87°編)
2022年1月15日
sin27°、cos27°、tan27°はどんな数?
PLUMBAGO関数...三角関数.三角比, 量...角度
Share:
https://p-suugaku.blogspot.com/2022/01/sin27cos27tan27.htmlsin27°、cos27°、tan27°はどんな数?
2022年1月14日
sin39°、cos39°、tan39°はどんな数?
PLUMBAGO関数...三角関数.三角比, 量...角度
Share:
https://p-suugaku.blogspot.com/2022/01/sin39cos39tan39.htmlsin39°、cos39°、tan39°はどんな数?
2022年1月13日
2次不等式を解く
PLUMBAGO式...不等式, 式...不等式...2次不等式, 手法
Share:
https://p-suugaku.blogspot.com/2022/01/2jifutoushiki-toku.html2次不等式を解く
sin33°、cos33°、tan33°はどんな数?
PLUMBAGO関数...三角関数.三角比, 量...角度
Share:
https://p-suugaku.blogspot.com/2022/01/sin33cos33tan33.htmlsin33°、cos33°、tan33°はどんな数?
2022年1月10日
2本の直線に挟まれた隣接する円の半径
PLUMBAGO幾何...円, 幾何...線...接線, 数列...等比数列
 |
| 図1 共通接線をもつ隣接する円 |
「60°の角度で交わる2本の直線を接線とする半径1の円$O_1$がある。また、2直線を共通の接線とし円$O_1$に接する円$O_2$、同じく2直線を共通の接線とし円$O_2$に接する円$O_3$…と図1のようにいくつもの円が並んでいる。このとき、
(1) 5番目の円$O_5$の半径を答えよ。
(2) $O_6$から$O_{10}$までの半径の和を答えよ。」
このような問題はどのように考えればよいでしょうか?
Share:
https://p-suugaku.blogspot.com/2022/01/rinsetsu-en-hankei.html2本の直線に挟まれた隣接する円の半径
sin42°、cos42°、tan42°はどんな数?
PLUMBAGO関数...三角関数.三角比, 量...角度
Share:
https://p-suugaku.blogspot.com/2022/01/sin42cos42tan42.htmlsin42°、cos42°、tan42°はどんな数?
sin21°、cos21°、tan21°はどんな数?
PLUMBAGO関数...三角関数.三角比, 量...角度
Share:
https://p-suugaku.blogspot.com/2022/01/sin21cos21tan21.htmlsin21°、cos21°、tan21°はどんな数?
2022年1月9日
すべての角が等しければ正多角形になるか?
PLUMBAGO幾何...多角形
正多角形には、
- すべての角が等しい。
- すべての辺の長さが等しい。
Share:
https://p-suugaku.blogspot.com/2022/01/seitakakukei.htmlすべての角が等しければ正多角形になるか?
2022年1月7日
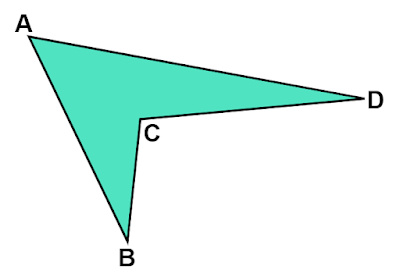
へこんでいる部分のある四角形の内角の和は何度?
Share:
https://p-suugaku.blogspot.com/2022/01/oushikakukei-naikaku.htmlへこんでいる部分のある四角形の内角の和は何度?
sin24°、cos24°、tan24°はどんな数?
PLUMBAGO関数...三角関数.三角比, 量...角度
Share:
https://p-suugaku.blogspot.com/2022/01/sin24cos24tan24.htmlsin24°、cos24°、tan24°はどんな数?
2022年1月6日
方べきの定理 なぜ成り立つ?
PLUMBAGO幾何...円, 幾何...合同.相似, 幾何...線...弦, 定理, 定理...方べきの定理
なぜ方べきの定理が成り立つのか調べてみました。
Share:
https://p-suugaku.blogspot.com/2022/01/houbeki-teiri.html方べきの定理 なぜ成り立つ?
同一円周上に4点がある場合とは?
PLUMBAGO幾何...円, 幾何...線...弦, 幾何...点, 定理, 定理...方べきの定理, 量...角度
4つの点にどういった関係が見られるとき同一円周上にあるということができるでしょうか?
Share:
https://p-suugaku.blogspot.com/2022/01/4.html同一円周上に4点がある場合とは?
2022年1月3日
2022年1月2日
循環小数と無限等比級数
PLUMBAGO数...実数...小数, 数列...等比数列
循環小数を等比数列の和で表すとどのようになるでしょうか?
Share:
https://p-suugaku.blogspot.com/2022/01/junkanshousuu-touhikyuusuu.html循環小数と無限等比級数
2022年1月1日
sin9°、cos9°、tan9°はどんな数?
PLUMBAGO関数...三角関数.三角比, 量...角度
Share:
https://p-suugaku.blogspot.com/2022/01/sin9-cos9-tan9.htmlsin9°、cos9°、tan9°はどんな数?
◎Amazonのアソシエイトとして、当サイト「数学について考えてみる」は適格販売により収入を得ています。

.png)