本記事では、実数解の個数が不明な2次方程式を因数分解以外の方法で解く方法を考えます。
1. 判別式を利用する
実数解の個数が不明な2次方程式の実数解を求められている場合の解答手順としては、
判別式で実数解の個数を調べる → 解の公式を使って解く
というのがひとつひとつ段階を踏んだ手順となります。
$ax^2+bx+c=0$の判別式$D$は
\[D=b^2-4ac\]
で表され、その値によって
a. $D>0$のとき、異なる2つの実数解をもつ。
b.
$D=0$のとき、だた1つの実数解をもつ。
c.
$D<0$のとき、実数解を持たない。
a.、b.のとき、すなわち$D\geqq0$のとき実数解をもつので解の公式を使って求めます。
$ax^2+bx+c=0$の解の公式は
$ax^2+bx+c=0$の解の公式は
\[x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}=\frac{-b\pm\sqrt{D}}{2a}\]
であるので、
例として$x^2+x-12=0$の場合、$a=1,b=1,c=-12$なので判別式$D$は
\[D=1^2-4\cdot1\cdot(-12)=49>0\]
となり、異なる2つの実数解を持ちます。
解は
\[x=\frac{-1\pm\sqrt{49}}{2}=\frac{-1\pm7}{2}=\mathbf{-4,3}\]
となります。
$x^2+x+5=0$の場合、$a=1,b=1,c=5$なので判別式$D$は
\[D=1^2-4\cdot1\cdot5=-19<0\]
となり、実数解を持ちません。
2. 解の公式を使う
判別式を利用せず、すぐに解の公式を使っても問題ありません。判別式を使わないことでより早く解を導き出すことができます。
$x^2+x+5=0$のように実数解を持たない場合は、
のように書けば対応できると思います。解の公式より
\[x=\frac{-1\pm\sqrt{-19}}{2}\]
根号の中が負となるため実数解を持たない。
1.でも同様に言えますが、複素数解も含めすべての解を求める場合は虚数$i$の定義
\[i=\sqrt{-1}\]
と、平方根の計算法則
\[\sqrt{ab}=\sqrt{a}×\sqrt{b}\]
を利用して、
\begin{align*}x&=\frac{-1\pm\sqrt{-19}}{2}\\[0.5em]&=\frac{-1\pm\sqrt{19}\cdot\sqrt{-1}}{2}\\[0.5em]&=\frac{-1\pm\sqrt{19}i}{2}=\frac{-1-\sqrt{19}i}{2},\frac{-1+\sqrt{19}i}{2}\end{align*}
のように解を求めることができます。
3. 平方完成を利用する
判別式を使わなくても平方完成で解くことも可能です。
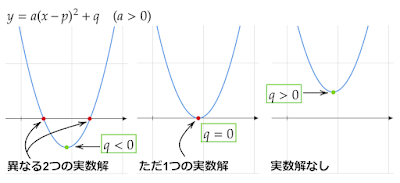
$ax^2+bx+c=a(x-p)^2+q$と平方完成できるとき、2次関数$y=a(x-p)^2+q$のグラフは頂点$(p,q)$が必ず$y$が最大値か最小値となる点になります。この頂点がどこにあるかを調べることが判別式の代わりとなります。
$a>0$のとき、下に凸の放物線を描き頂点$(p,q)$は$y$が最小となる点であるので、
a.
$q<0$のとき、x軸($y=0$)と交わるので異なる2つの実数解を持ちます。
b.
$q=0$のとき、x軸と接するのでただ1つの実数解を持ちます。
c.
$q>0$のとき、x軸と交わりも接しもしないため実数解を持ちません。
$a<0$のとき、上に凸の放物線を描き頂点は$y$が最大となる点であるので、
d.
$q>0$のとき、x軸と交わるので異なる2つの実数解を持ちます。
e.
$q=0$のとき、x軸と接するのでただ1つの実数解を持ちます。
f.
$q<0$のとき、x軸と交わりも接しもしないため実数解を持ちません。
以上の6通りで実数解の個数を判別できますが、$a<0$のときは方程式の$x^2$の係数が正になるように両辺に$-1$を掛けると、2次関数は下に凸の放物線になるのでa.、b.、c.の3通りに絞り込むことができます。
例として$x^2+x-5=0$の場合は、平方完成すると
\[\left(x+\frac{1}{2}\right)^2-\frac{21}{4}=0\]
となり、$y=\left(x+\dfrac{1}{2}\right)^2-\dfrac{21}{4}$は下に凸の放物線で$-\dfrac{21}{4}<0$であるので、a.に該当し異なる2つの実数解を持ちます。
その実数解は、平方完成した方程式を移項して
\[\left(x+\frac{1}{2}\right)^2=\frac{21}{4}\]
$x+\dfrac{1}{2}=t$とおくと、
\begin{align*}t^2&=\frac{21}{4}\\[0.5em]t&=\pm\sqrt{\frac{21}{4}}\\[0.5em]&=\pm\frac{\sqrt{21}}{2}\end{align*}
$t$を戻して
\begin{align*}x+\frac{1}{2}&=\pm\frac{\sqrt{21}}{2}\\[0.5em]x&=-\frac{1}{2}\pm\frac{\sqrt{21}}{2}\\[0.5em]&=-\frac{1+\sqrt{21}}{2},\frac{-1+\sqrt{21}}{2}\end{align*}
となります。
$-x^2-x-5=0$の場合は、両辺に$-1$を掛けて
\[x^2+x+5=0\]
これを平方完成すると
\[\left(x+\frac{1}{2}\right)^2+\frac{19}{4}=0\]
となり、$y=\left(x+\dfrac{1}{2}\right)^2+\dfrac{19}{4}$は上に凸の放物線で$\dfrac{19}{4}>0$であるので、c.に該当し実数解を持ちません。両辺に$-1$を掛けなかったときはf.に該当し、この場合でも実数解を持たないことがわかります。
ここから複素数解を求めるときは
\begin{align*}\left(x+\frac{1}{2}\right)^2&=-\frac{19}{4}\end{align*}
$x+\dfrac{1}{2}=t$とおくと、
\begin{align*}t^2&=-\frac{19}{4}\\[0.5em]t&=\pm\sqrt{\frac{\mathbf{-19}}{4}}&\textbf{注意}\\[0.5em]&=\pm\frac{\sqrt{19}i}{2}\end{align*}
$t$を戻して
\begin{align*}x+\frac{1}{2}&=\pm\frac{\sqrt{19}i}{2}\\[0.5em]x&=-\frac{1}{2}\pm\frac{\sqrt{19}i}{2}\\[0.5em]&=\frac{-1-\sqrt{19}i}{2},\frac{-1+\sqrt{19}i}{2}\end{align*}
となります。
Share: