Geometric mean theorem（幾何平均定理）

　幾何平均定理（Geometric mean theorem）がなぜ成立するのかを確かめてみました。

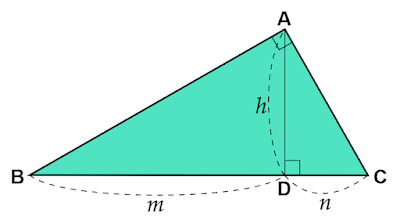
　幾何平均定理とは、$∠\text{A}=90°$となる直角三角形$\text{ABC}$の頂点$\text{A}$から$\text{BC}$に垂線を下ろしその交点を$\text{D}$とします。垂線$\text{AD}$の長さを$h$、$\text{BD, DC}$の長さをそれぞれ$m, n$とすると、これらの関係は

$$h=\sqrt{mn}$$

となるという定理です。

これが成立することを確かめてみます。

　$△\text{ABD}$と$△\text{CAD}$に着目します。

$$∠\text{ADB}=∠\text{CDA}=90°\tag{a}$$

で、三角形の内角の和は$180°$であるから

$$\begin{align*}∠\text{ABD}+∠\text{BAD}&=90°\tag{b}\\[1em]∠\text{CAD}+∠\text{ACD}&=90°\tag{c}\end{align*}$$

また、$△\text{ABC}$において$∠\text{BAC}=90°$であるから

$$∠\text{ABC}+∠\text{ACB}=90°$$

$∠\text{ABC}$と$∠\text{ABD}$、$∠\text{ACB}$と$∠\text{ACD}$は共通の角であるから

$$∠\text{ABD}+∠\text{ACD}=90°\tag{d}$$

$\text{(b), (d)}$より

$$∠\text{BAD}=∠\text{ACD}\tag{e}$$

$\text{(c), (d)}$より

$$∠\text{ABD}=∠\text{CAD}\tag{f}$$

$\text{(a), (e), (f)}$より3組の角が等しいので$△\text{ABD}$と$△\text{CAD}$は相似です。

相似な図形の対応する2辺の比は等しいので

$$\begin{align*}\text{AD}:\text{BD}&=\text{CD}:\text{AD}\\[0.5em]h:m&=n:h\\[0.5em]h^2&=mn\\[0.5em]h&=\sqrt{mn}&(\because h>0)\end{align*}$$

となり、幾何平均定理が成り立つことがわかります。

関連：相似な三角形の辺の比

　幾何平均は相乗平均とも言います。相乗平均といえば「相加平均と相乗平均の大小関係」があります。これに対しこの幾何平均定理を利用して図形をもちいた説明を与えることができます。

直角三角形の外接円を考えると斜辺は外接円の直径になることに着目します。

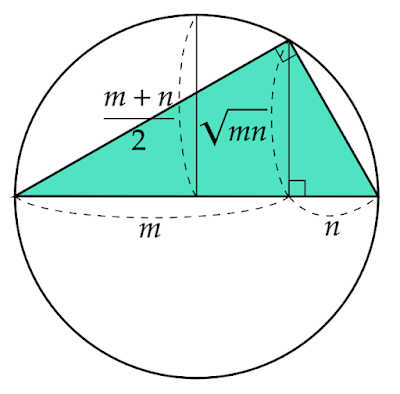
斜辺が直角からの垂線との交点によって長さが$m, n$に分けられているとすると
外接円の直径は$m+n$であるから半径は$\dfrac{m+n}{2}$、
直角三角形の垂線の長さは幾何平均定理より$\sqrt{mn}$となります。

垂線の長さは半径を最大としてそれ以上の長さになることはないので

$$\frac{m+n}{2}\geqq\sqrt{mn}$$

が成り立ちます。

垂線の長さが半径と等しくなるとき、直角三角形は直角二等辺三角形となり垂線は斜辺に対する垂直二等分線となるため、

$$\begin{align*}m=nのとき\\ &\frac{m+n}{2}=\sqrt{mn}\end{align*}$$

となることがわかります。

外部リンク：Geometric mean theorem - Wikipedia

関連：相加平均と相乗平均　なぜa=bなのか　最大値か最小値か

関連：2数、3数の場合の相加平均と相乗平均の大小関係

幾何の有名な定理 (数学ワンポイント双書 36)

Amazonで見る楽天市場で見るYahoo!ショッピングで見る