面積の等しい三角形の作図（三角形の等積変形）

図1　$△\text{ABC}$

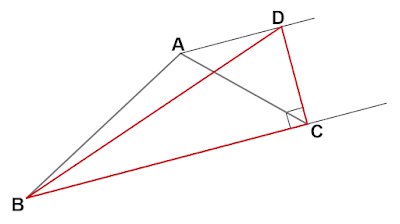
「図1の$△\text{ABC}$を以下の条件で等積変形した三角形を定規とコンパスで作図せよ。

(1)$∠\text{BCD}=90°$となる直角三角形$\text{DBC}$

(2)$\text{AB}=\text{BE}$となる二等辺三角形$\text{ABE}$

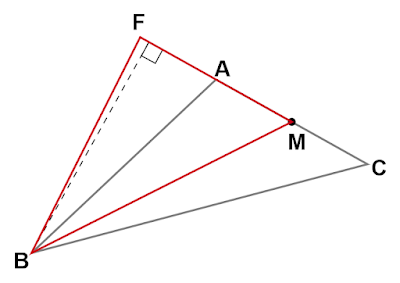
(3)辺$\text{AC}$を底辺としたとき$△\text{ABC}$と高さが等しい$△\text{FBM}$
ただし、頂点$\text{M}$は辺$\text{AC}$の中点である」

このような問題はどのように解けばよいでしょうか？

(1)$∠\text{BCD}=90°$となる直角三角形$\text{DBC}$

1.

辺$\text{BC}$の$\text{C}$の側を延長し、$\text{BC}$に平行な直線を頂点$\text{A}$を通るように引きます。

2.

頂点$\text{C}$を中心に円弧を描き、半直線$\text{BC}$との交点を$a, b$とします。
半径が等しい円弧を点$a, b$それぞれを中心として描き$\text{BC}$に対する垂線を作図し、点$\text{A}$を通る平行線との交点を$\text{D}$とします。

3.

$△\text{DBC}$を描きます。
頂点$\text{A}$を辺$\text{BC}$に平行な直線上の点$\text{D}$まで移動させているので$△\text{ABC}$と$△\text{DBC}$の面積は等しいです。

(2)$\text{AB}=\text{BE}$となる二等辺三角形$\text{ABE}$

1.

辺$\text{AB}$に平行な直線を頂点$\text{C}$を通るように引きます。

2.

$\text{AB}$の長さを半径とする円弧を頂点$\text{B}$を中心として描き、頂点$\text{C}$を通る平行線との交点を$\text{E}$とします。
線分$\text{BE}$を引きます。

3.

$△\text{ABE}$を描きます。
頂点$\text{C}$を辺$\text{AB}$に平行な直線上の点\text{E}まで移動させているので$△\text{ABC}$と$△\text{ABE}$の面積は等しいです。

(3)$△\text{ABC}$と高さが等しい$△\text{FBM}$

1.

頂点$\text{A, C}$それぞれを中心として半径の等しい円弧を描き、辺$\text{AC}$の垂直二等分線を作図します。辺$\text{AC}$とその垂直二等分線との交点を$\text{M}$とします。

2.

辺$\text{AC}$の$\text{A}$の側を延長し、$\text{AC}$の長さを半径とする円弧を点$\text{M}$を中心として描き、半直線$\text{CA}$との交点を$\text{F}$とします。

3.

$△\text{FBM}$を描きます。
辺$\text{FM}$は辺$\text{AC}$の長さを変えずに直線$\text{AC}$上を移動させたものなので頂点$\text{B}$との距離は変わりません、すなわち辺$\text{AC, FM}$をそれぞれ底辺としたとき$△\text{ABC}$と$△\text{FBM}$の高さが等しいので面積も等しいです。

2.で辺$\text{AC}$の$\text{C}$の側を延長した場合も同様に等積変形でき、これは別解となります。

関連：三角形の等積変形