.png)
|
| 図1 正三角形の各部分の面積比は? |
このような問題はどのように解けばよいでしょうか?

|
| 図2 $\text{AG, BG, CG}$で分割 |
すると緑の四角形は$□\text{ADGF}$、赤い四角形は$□\text{BEGD}$、青い四角形は$□\text{CFGE}$となるので、$□\text{ADGF}:□\text{BEGD}:□\text{CFGE}$を求めることになります。
線分$\text{AG, BG, CG}$を引き、$△\text{GAB, }△\text{GBC, }△\text{GCA}$に分割します。これらの三角形は合同なので面積は等しいです。
またこうして分割すると各四角形の面積は
\begin{align*}□\text{ADGF}&=△\text{GAD}+△\text{GFA}\tag{a}\\[1em]□\text{BEGD}&=△\text{GBE}+△\text{GDB}\tag{b}\\[1em]□\text{CFGE}&=△\text{GCF}+△\text{GEC}\tag{c}\end{align*}
となります。

|
| 図3 $△\text{GAB}$ |
辺$\text{AB}$を底辺とすると$△\text{GAD}$と$△\text{GDB}$は高さが同じなので底辺の長さの比と面積比は等しくなります。したがって
\[△\text{GAD}:△\text{GDB}=5:1\]
また、$△\text{GAB}$の面積を$\text{S}$とおけば
\begin{align*}△\text{GAD}&=\frac{5}{6}\text{S}\tag1\\[1em]△\text{GDB}&=\frac{1}{6}\text{S}\tag2\end{align*}
となります。
|
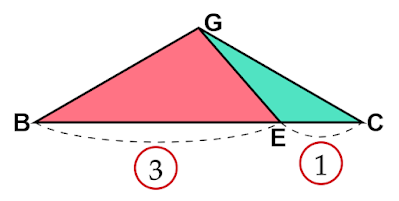
| 図4 $△\text{GBC}$ |
$△\text{GAB}$のときと同様、辺$\text{BC}$を底辺とすれば$△\text{GBE}$と$△\text{GEC}$の面積比は底辺の長さの比と等しくなるので
\[△\text{GBE}:△\text{GEC}=3:1\]
$△\text{GBC}$の面積は$△\text{GAB}$と等しいのでこれを$\text{S}$とおけば
\begin{align*}△\text{GBE}&=\frac{3}{4}\text{S}\tag3\\[1em]△\text{GEC}&=\frac{1}{4}\text{S}\tag4\end{align*}
となります。

|
| 図5 $△\text{GCA}$ |
これも$△\text{GAB}$と同様、$△\text{GCF}$と$△\text{GFA}$の面積比は$\text{CA}$の内分比と等しくなるので
\[△\text{GCF}:△\text{GFA}=4:1\]
$△\text{GCA}$の面積も$△\text{GAB}$と等しいので$\text{S}$をもちいれば
\begin{align*}△\text{GCF}&=\frac{4}{5}\text{S}\tag5\\[1em]△\text{GFA}&=\frac{1}{5}\text{S}\tag6\end{align*}
となります。
$\text{(a), (b), (c)}$に$(1), (2), (3), (4), (5), (6)$を代入すると
\begin{align*}□\text{ADGF}&=\frac{5}{6}\text{S}+\frac{1}{5}\text{S}\\[0.5em]&=\frac{31}{30}\text{S}\\[1em]□\text{BEGD}&=\frac{1}{6}\text{S}+\frac{3}{4}\text{S}\\[0.5em]&=\frac{11}{12}\text{S}\\[1em]□\text{CFGE}&=\frac{1}{4}\text{S}+\frac{4}{5}\text{S}\\[0.5em]&=\frac{21}{20}\text{S}\end{align*}
となるので、求める面積比は
\begin{align*}□\text{ADGF}:□\text{BEGD}:□\text{CFGE}&=\frac{31}{30}\text{S}:\frac{11}{12}\text{S}:\frac{21}{20}\text{S}\\[0.5em]&=\underline{62:55:63}\end{align*}
となります。
Share:



