|
| 図1 ナポレオンの定理 |
|
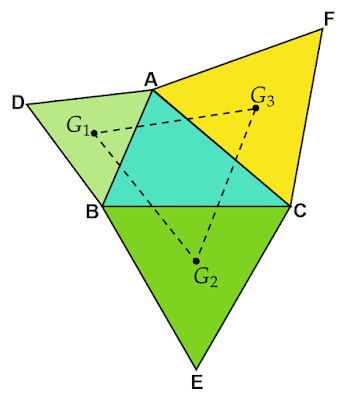
| 図2 △ABCとベクトル |
\begin{gather*}&\vec{A}\neq k\vec{B}かつ\vec{B}\neq
l\vec{C}かつ\vec{C}\neq m\vec{A}\\[0.5em] &\vec{AB}\neq
k\vec{BC}または\vec{BC}\neq k\vec{CA}または\vec{CA}\neq
k\vec{AB}\end{gather*}
|
| 図3 \vec{OG_1}を構成するベクトル |
\vec{AB}は
\begin{align*}\vec{AB}&=\vec{B}-\vec{A}\\[0.5em] &=(x_2 -x_1,y_2
-y_1)\end{align*}
ABの中点をHとして\vec{AH}は
\begin{align*}\vec{AH}&=\frac{1}{2}\vec{AB}\\[0.5em]
&=\frac{\vec{B}-\vec{A}}{2}\\[0.5em]&=\left(\frac{x_2
-x_1}{2},\frac{y_2 -y_1}{2}\right)\end{align*}
\vec{HG_1}は\vec{AH}に垂直です。また、DHはAHの\sqrt{3}倍で点G_1はDHを2:1に内分します。
ここで、\vec{X}に垂直で大きさが等しいベクトルを\vec{X}^Vと表記することにして
\begin{align*}\vec{HG_1}&=\frac{\sqrt{3}}{3}\vec{AH}^V\\[0.5em]
&=\frac{\sqrt{3}}{3}\left(\frac{\vec{B}-\vec{A}}{2}\right)^V\end{align*}
このベクトル成分は、図3より\vec{AH}の向きと比較して\vec{HG_1}は時計回りの回転をしているから
\vec{X}=(x,y)\Rightarrow\vec{X}^V=(-y,x)
とすれば良いので
\begin{align*}\vec{HG_1}&=\frac{\sqrt{3}}{3}\left(\frac{y_1
-y_2}{2},\frac{x_2 -x_1}{2}\right)\\[0.5em]&=\left(\frac{\sqrt{3}(y_1
-y_2)}{6},\frac{\sqrt{3}(x_2 -x_1)}{6}\right)\end{align*}
したがって\vec{OG_1}は
\begin{align*}\vec{OG_1}&=\vec{A}+\vec{AH}+\vec{HG_1}\\[0.5em]
&=\left(\frac{3(x_1+x_2)+\sqrt{3}(y_1-y_2)}{6},\frac{3(y_1+y_2)+\sqrt{3}(x_2-x_1)}{6}\right)\end{align*}
また、\dfrac{\sqrt{3}}{6}x_n=s_n,\dfrac{\sqrt{3}}{6}y_n=t_nとおけば
\vec{OG_1}=(\sqrt{3}(s_1+s_2)+t_1-t_2,\sqrt{3}(t_1+t_2)+s_2-s_1)
と表すことができます。
\vec{OG_2}の成分の場合はs_1,s_2,t_1,t_2をそれぞれs_2,s_3,t_2,t_3へ、\vec{OG_3}の成分の場合はそれぞれs_3,s_1,t_3,t_1へ置き換えれば良いので
\begin{align*}\vec{OG_2}&=(\sqrt{3}(s_2+s_3)+t_2-t_3,\sqrt{3}(t_2+t_2)+s_3-s_2)\\[1em]\vec{OG_3}&=(\sqrt{3}(s_3+s_1)+t_3-t_1,\sqrt{3}(t_3+t_1)+s_1-s_3)\end{align*}
となります。
以上から\vec{G_1 G_2},\vec{G_1 G_3}は
\begin{align*}\vec{G_1
G_2}&=(\sqrt{3}(s_3-s_1)-t_1+2t_2-t_3,\sqrt{3}(t_3-t_1)+s_1-2s_2+s_3)\\[1em]\vec{G_1
G_3}&=(\sqrt{3}(s_3-s_2)-2t_1+t_2+t_3,\sqrt{3}(t_3-t_2)+2s_1-s_2-s_3)\end{align*}
と表わせます。
\vec{G_1 G_2},\vec{G_1
G_3}を使ってナポレオンの定理が正しいことを確かめるには、ベクトルの内積
\begin{align*}\vec{X}=(x,y),&\vec{Y}=(p,q)\\[0.5em]
\vec{X}\cdot\vec{Y}&=px+qy\\[0.5em]
&=|\vec{X}||\vec{Y}|\cos\theta\end{align*}
より\cos\theta=\dfrac{px+qy}{|\vec{X}||\vec{Y}|}。
この式から\theta=60°であることと|\vec{X}|=|\vec{Y}|であることが示せれば良いので、内積と各ベクトルの大きさを調べてみます。
（これは△G_1 G_2
G_3が頂角60°の二等辺三角形であることを示すことで正三角形であることが示されることに相当します。）
\begin{align*}\vec{G_1 G_2}\cdot\vec{G_1
G_3}&=\{\sqrt{3}(s_3-s_1)-t_1+2t_2-t_3\}\{\sqrt{3}(s_3-s_2)-2t_1+t_2+t_3\}\\
&\quad+\{\sqrt{3}(t_3-t_1)+s_1-2s_2+s_3\}\{\sqrt{3}(t_3-t_2)+2s_1-s_2-s_3\}\\[0.5em]&=2\{{s_1}^2+{s_2}^2+{s_3}^2-s_1
s_2-s_2 s_3-s_3 s_1\\ &\quad-\sqrt{3}(s_1 t_2-s_1 t_3-s_2 t_1+s_2
t_3+s_3 t_1-s_3 t_2)\\ &\quad+{t_1}^2+{t_2}^2+{t_3}^2-t_1 t_2-t_2
t_3-t_3 t_1\}\\[1.5em]|\vec{G_1
G_2}|&=[\{\sqrt{3}(s_3-s_1)-t_1+2t_2-t_3\}^2\\
&\quad+\{\sqrt{3}(t_3-t_1)+s_1-2s_2+s_3\}^2]^\frac{1}{2}\\[0.5em]&=2\{{s_1}^2+{s_2}^2+{s_3}^2-s_1
s_2-s_2 s_3-s_3 s_1\\ &\quad-\sqrt{3}(s_1 t_2-s_1 t_3-s_2 t_1+s_2
t_3+s_3 t_1-s_3 t_2)\\ &\quad+{t_1}^2+{t_2}^2+{t_3}^2-t_1 t_2-t_2
t_3-t_3 t_1\}^{\frac{1}{2}}\\[1.5em]|\vec{G_1
G_3}|&=[\{\sqrt{3}(s_3-s_2)-2t_1+t_2+t_3\}^2\\
&\quad+\{\sqrt{3}(t_3-t_2)+2s_1-s_2-s_3\}^2]^\frac{1}{2}\\[0.5em]&=2\{{s_1}^2+{s_2}^2+{s_3}^2-s_1
s_2-s_2 s_3-s_3 s_1\\ &\quad-\sqrt{3}(s_1 t_2-s_1 t_3-s_2 t_1+s_2
t_3+s_3 t_1-s_3 t_2)\\ &\quad+{t_1}^2+{t_2}^2+{t_3}^2-t_1 t_2-t_2
t_3-t_3 t_1\}^{\frac{1}{2}}\end{align*}
ここで
\begin{align*}u&={s_1}^2+{s_2}^2+{s_3}^2-s_1 s_2-s_2 s_3-s_3 s_1\\
&\quad-\sqrt{3}(s_1 t_2-s_1 t_3-s_2 t_1+s_2 t_3+s_3 t_1-s_3 t_2)\\
&\quad+{t_1}^2+{t_2}^2+{t_3}^2-t_1 t_2-t_2 t_3-t_3 t_1\end{align*}
とおけば
\begin{align*}|\vec{G_1 G_2}|&=|\vec{G_1
G_3}|=2\sqrt{u}\\[0.5em]
\cos\theta&=\frac{2u}{2\sqrt{u}\cdot2\sqrt{u}}\\[0.5em]&=\frac{1}{2}\\[0.5em]\theta&=60°\end{align*}
となるので、ナポレオンの定理が正しいことを確かめることができました。
以下に紹介する動画のような方法でもナポレオンの定理の証明ができます。
外部リンク：Napoleon's theorem | Proof | - YouTube
外部リンク：ナポレオンの定理 - Wikipedia
Share:
