角の二等分ベクトルはどうやって求める？

　角の二等分ベクトルはどのように求めるのでしょうか？

角の二等分ベクトルを角の二等分線の作図法を参考に2通りの方法で求めてみます。

関連：角の二等分線の作図法

2つの異なるベクトル$\vec{a},\vec{b}$について考えます。
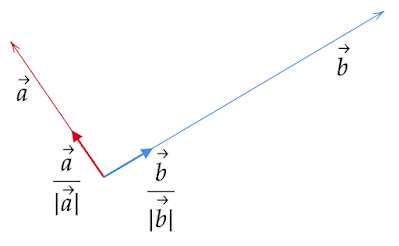
角の二等分線の作図法を参考にすると、まずは大きさが同じで$\vec{a},\vec{b}$とそれぞれ向きが同じであるベクトルをおく必要があります。

したがって、$\vec{a},\vec{b}$それぞれの単位ベクトル$\dfrac{\vec{a}}{|\vec{a}|},\dfrac{\vec{b}}{|\vec{b}|}$をおきます。各ベクトル自身の大きさで割っている（実数倍している）ので各単位ベクトルの向きはそれぞれ$\vec{a},\vec{b}$と同じで大きさは$1$になります。

ここから2通りの方法で求めてみます。

1. 二等辺三角形の利用

2つの単位ベクトルの差は$\dfrac{\vec{a}}{|\vec{a}|}-\dfrac{\vec{b}}{|\vec{b}|}$と書けます。
$\dfrac{\vec{a}}{|\vec{a}|},\dfrac{\vec{b}}{|\vec{b}|},\dfrac{\vec{a}}{|\vec{a}|}-\dfrac{\vec{b}}{|\vec{b}|}$の3ベクトルによって二等辺三角形ができ、$\vec{a},\vec{b}$の始点である頂点からのびる中線は垂直二等分線であり、かつ求める角の二等分線（角の二等分ベクトル）です。

このことから、角の二等分ベクトル$\vec{p}$は$\vec{b}$と$\dfrac{1}{2}\left(\dfrac{\vec{a}}{|\vec{a}|}-\dfrac{\vec{b}}{|\vec{b}|}\right)$の合成で表されるので

\begin{align*}\vec{p}&=\vec{b}+\frac{1}{2}\left(\frac{\vec{a}}{|\vec{a}|}-\frac{\vec{b}}{|\vec{b}|}\right)\\[0.5em]&=\frac{\vec{a}}{2|\vec{a}|}+\frac{\vec{b}}{2|\vec{b}|}\\[0.5em]&=\frac{1}{2}\left(\frac{\vec{a}}{|\vec{a}|}+\frac{\vec{b}}{|\vec{b}|}\right)\end{align*}

実数倍したベクトルも元のベクトルと向きは同じなので係数を$1$にするために2倍した角の二等分ベクトル$\vec{P}$は

\begin{align*}\vec{P}&=2\vec{p}\\[0.5em]&=\frac{\vec{a}}{|\vec{a}|}+\frac{\vec{b}}{|\vec{b}|}\end{align*}

となります。

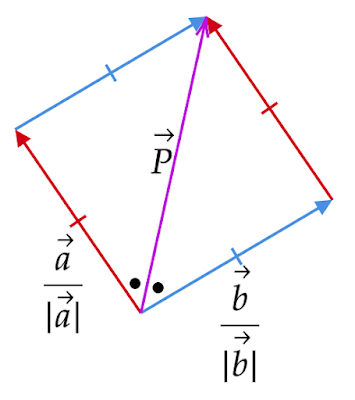
2. ひし形の利用

$\vec{a}$の単位ベクトルの終点に$\vec{b}$の単位ベクトルを移動、あるいは$\vec{b}$の単位ベクトルの終点に$\vec{a}$の単位ベクトルを移動させます。
すると、2つの単位ベクトルの和はひし形の対角線にあたります。ひし形の対角線は2つの単位ベクトルのなす角の二等分線であるので、角の二等分ベクトル$\vec{P}$は

\[\vec{P}=\frac{\vec{a}}{|\vec{a}|}+\frac{\vec{b}}{|\vec{b}|}\]

となります。

関連：ひし形の対角線がひし形の内角の二等分線であることを確かめてみる

　以上から、2つの異なるベクトル$\vec{a},\vec{b}$の角の二等分ベクトルは

\[\frac{\vec{a}}{|\vec{a}|}+\frac{\vec{b}}{|\vec{b}|}\]

で求められることがわかりました。

リンク