平行四辺形の中の図形の面積

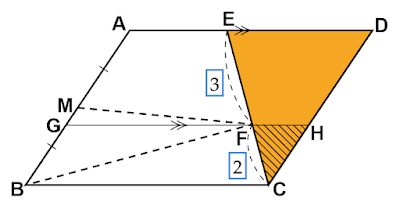
図1　平行四辺形$\text{ABCD}$

「図1のように平行四辺形$\text{ABCD}$がある。辺$\text{AD}$を$2:3$に内分する点$\text{E}$をおき、線分$\text{CE}$を引く。また、$\text{CE}$を$2:3$に内分する点$\text{F}$をおく。さらに辺$\text{AB}$の中点$\text{M}$をおく。
平行四辺形の面積を$S$としたとき、図1の青い部分、$□\text{AMFE}$と$△\text{BCF}$の面積の和を$S$をもちいて表わせ。」

このような問題はどのように解けばよいでしょうか？

　図1の平行四辺形の青い部分の面積を求める問題ですが、平行四辺形$\text{ABCD}$の面積から白い部分、$△\text{ECD}$と$△\text{MBF}$の面積を引くことで求めます。

　$△\text{ECD}$の面積を求めます。

図2　$△\text{ACD}$と$△\text{ECD}$

$\text{AC}$を引き、$△\text{ACD}$と$△\text{ECD}$を比較すると$\text{AD, ED}$を底辺とすれば高さが同じなので面積比は底辺の長さの比と等しくなります。
$\text{AE}:\text{ED}=2:3$より$\text{AD}:\text{ED}=5:3$なので

$$\begin{align*}△\text{ACD}:△\text{ECD}&=5:3\\[0.5em]△\text{ECD}&=\frac{3}{5}△\text{ACD}\end{align*}$$

△\text{ACD}の面積は平行四辺形\text{ABCD}の面積の半分なので

$$\begin{align*}△\text{ECD}&=\frac{3}{5}×\frac{1}{2}S\\[0.5em]&=\frac{3}{10}S\end{align*}$$

　$△\text{MBF}$の面積を求めます。

図3　$\text{GH}$を引く

点$\text{F}$を通る$\text{AD}$に平行な直線を引き、$\text{AB}$との交点を$\text{G}$、$\text{CD}$との交点を$\text{H}$とします。

ここで$△\text{CDE}$と$△\text{CHF}$に着目すると$∠\text{FCH}$が共通で平行線の同位角より

$$\begin{align*}∠\text{CHF}&=∠\text{CDE}\\[0.5em]∠\text{CFH}&=∠\text{CED}\end{align*}$$

であるから、3組の角が等しいので相似です。

その相似比は$\text{CF}:\text{FE}=2:3$より$\text{CE}:\text{CF}=5:2$なので

$$\begin{align*}\text{ED}:\text{FH}&=5:2\\[0.5em]\text{FH}&=\frac{2}{5}\text{ED}\end{align*}$$

前述より$\text{AD}:\text{ED}=5:3$なので

$$\begin{align*}\text{FH}&=\frac{2}{5}×\frac{3}{5}\text{AD}\\[0.5em]&=\frac{6}{25}\text{AD}\end{align*}$$

$\text{AD}=\text{GH}$なので

$$\text{GH}:\text{GF}=25:19$$$

これで$△\text{MBF}$の辺$\text{MB}$を底辺としたとき$\text{GH}:\text{GF}$という高さっぽいものの比が求められたので高さとの関連を調べてみます。

図4　$△\text{FGJ}$と$△\text{HGI}$

点$\text{H, F}$からそれぞれ直線$\text{AB}$に対し垂線をおろし、$\text{AB}$との交点を$\text{I, J}$とします。すると直線$\text{AB}$上にある辺をを底辺とすると$\text{HI}$の長さは平行四辺形$\text{ABCD}$の高さ、$\text{FJ}$の長さは$△\text{FJG}$の高さであり$△\text{MBF}$の高さでもあります。

$△\text{HIG}$と$△\text{FJG}$について考えると$∠\text{IGH}$は共通で

$$\begin{align*}∠\text{HIG}&=∠\text{FJG}=90°\\[0.5em]∠\text{IGH-}90°&=∠\text{IHG}=∠\text{JFG}\end{align*}$$

であるから、3組の角が等しいので相似です。

その相似比は$\text{GH}:\text{GF}=25:19$なので

$$\text{JF}=\frac{19}{25}\text{HI}$$

つまり、高さの比と$\text{GH}:\text{GF}$は等しいことがわかります。

すると$△\text{MBF}$の面積は底辺は$\text{AB}$の半分の長さで、高さは平行四辺形$\text{ABCD}$の$\dfrac{19}{25}$また$S=\text{AB}×\text{HI}$なので、

$$\begin{align*}△\text{MBF}&=\frac{1}{2}×\frac{1}{2}\text{AB}×\frac{19}{25}\text{HI}\\[0.5em]&=\frac{19}{100}S\end{align*}$$

　したがって図1の青い部分、すなわち$□\text{AMFE}$と$△\text{BCF}$の面積の和は

$$\begin{align*}□\text{AMFE}+△\text{BCF}&=□\text{ABCD-}△\text{ECD-}△\text{MBF}\\[0.5em]&=S-\frac{3}{10}S-\frac{19}{100}S\\[0.5em]&=S-\frac{30}{100}S-\frac{19}{100}S\\[0.5em]&=\frac{51}{100}S\end{align*}$$

となります。

関連：平行四辺形の中の三角形の面積