絶対値のある2次方程式の実数解の個数

「$|x^2-3x-18|=x+k$が実数解をもつときの$k$の値の範囲を実数解の個数ごとに場合分けをして答えよ。」

このような問題はどのように解けばよいでしょうか？

　この方程式は連立方程式

\begin{cases}y=|x^2-3x-18|\\[0.5em] y=x+k\end{cases}

からできたものと考え、この2関数のグラフから共有点の個数を調べてみます。

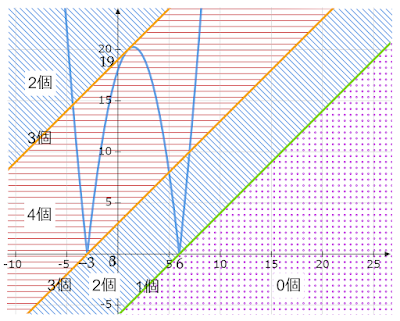
図1　$y=|x^2-3x-18|$と$y=x+k$

　$y=|x^2-3x-18|$のグラフは、絶対値の中の$x^2-3x-18$を因数分解すると$(x+3)(x-6)$になるため、x軸との共有点は$(-3,0),(6,0)$であることがわかります。また、下に凸の放物線であるため$-3<x<6$の範囲において$x^2-3x-18<0$となります。
しかし、$|x^2-3x-18|\geqq0$であるため$-3<x<6$のとき$|x^2-3x-18|=-(x^2-3x-18)$となります。したがって、

\begin{align*}y&=|x^2-3x-18|\\ &\Leftrightarrow\begin{cases}y=x^2-3-18&(x\leqq-3,6\leqq x)\\[0.5em] y=-(x^2-3x-18)\\ \quad=-x^2+3x+18&(-3<x<6)\end{cases}\end{align*}

となります。
このグラフは図1の青線となります。

　$y=x$を平行移動、すなわちy切片となる$y=x+k$の$k$の値を変化させて$y=|x^2-3x-18|$との共有点の個数を見ていくと、
$y=x+k$が$(6,0)$を通るとき、すなわち

\begin{align*}0&=6+k\\[0.5em] k&=-6\tag{a}\end{align*}

のとき、共有点は1個。
このときの$y=x+k$のグラフは図1の緑線です。

$k$が$(a)$より小さくなる、すなわち$k<-6$のとき共有点は0個。
このとき$y=x+k$のグラフは右下のドット柄の範囲にあります。

$y=x+k$が$(-3,0)$を通るとき、すなわち

\begin{align*}0&=-3+k\\[0.5em] k&=3\tag{b}\end{align*}

のとき、共有点は3個。
このとき$y=x+k$のグラフは図1の$(-3,0)$を通る方のオレンジ線です。

$k$が$(a)$と$(b)$の間、すなわち$-6<k<3$のとき共有点は2個。
このとき$y=x+k$のグラフは図1右下の青い縞柄の範囲にあります。

$y=x+k$が$y=-x^2+3x+18\ (-3<x<6)$と接するとき共有点は3個。

このときの$k$の値は、共有点を求める連立方程式

\begin{cases}y=-x^2+3x+18\\[0.5em] y=x+k\end{cases}

より$x^2-2x-18+k=0$が得られるので、判別式をもちいて

\[D=(-2)^2-4\cdot1\cdot(-18+k)=76-4k\]

2次関数と1次関数が接するとき$D=0$を調べれば良いので

\begin{align*}D=76-4k&=0\\[0.5em] k&=19\tag{c}\end{align*}

であることがわかります。

このとき、$y=x+k$のグラフは図1左上のオレンジ線です。

$k$が$(b)$と$(c)$の間、すなわち$3<k<19$のとき共有点は4個。
このとき$y=x+k$のグラフは図1の赤い横縞柄の範囲にあります。

$k$が$(c)$より大きいとき、すなわち$k>19$のとき共有点は2個。
このとき$y=x+k$のグラフは図1左上の青い縞柄の範囲にあります。

　共有点の個数はそれぞれの$k$の値のときの実数解の個数となるため以上をまとめると

• 実数解が0個のとき$k<-6$
• 実数解が1個のとき$k=-6$
• 実数解が2個のとき$-6<k<3,19<k$
• 実数解が3個のとき$k=3,19$
• 実数解が4個のとき$3<k<19$

となります。

求める答えは実数解をもつときの$k$の値の範囲なので、実数解が0個のときを除いたものが答えとなります。

関連：絶対値のある2次方程式の実数解の個数（グラフ不使用）