どっちが分子でどっちが分母？

　分数の分子と分母、どちらなのか迷ってしまうものがあると思います。 割り算、横書きの分数、比の値。そして三角比。それぞれどちらが分子、分母になるのかを見ていきます。 ...

Read More

鎖の輪のように連なる円の面積の差

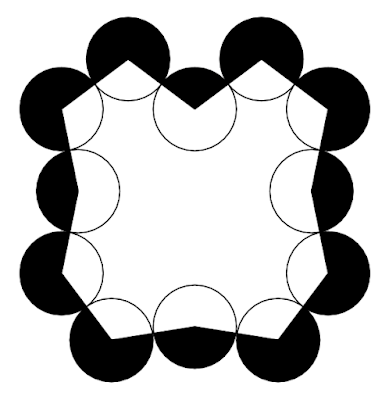図1　鎖の輪状に連なる円　「図1のように同じ半径の円が鎖の輪のように連なっている。それぞれの円の中心を線でつないでできる図形の内側にある方を白く、外側にある方を黒く円を塗り分けた。円の黒い部分の合計と白い部分の合計の面積の差はいくらになるか。1つの円の面積を1とする。」このような問題をどのように解けばよいかを考えてみ...

Read More

三角形の角の二等分線と線分の比 本当に成立する？

「$△\text{ABC}$の$\text{AB}=a, \text{AC}=b$として、$∠\text{A}$の二等分線と辺$\text{BC}$との交点$\text{P}$は、辺$\text{BC}$を$a:b$に内分する。また、$\text{AB}≠\text{AC}$である$△\text{ABC}$の$∠\text{A}$の外角の二等分線と辺$\text{BC}$の延長線との交点$\text{Q}$は、辺$\text{BC}$を$a:b$に外分する。」という性質があります。 本当にこれが成立するのかを証明してみます。 ...

Read More

直交する弦の長さから円の半径を求める

　円の中心を通らない直交する2本の弦$\text{AB,CD}$の各部分の長さのみがわかっているとき、円の半径を求めるにはどうすればよいでしょうか?このとき、弦$\text{AB,CD}$の交点を$\text{P}$、線分$\text{AP,BP,CP,DP}$の長さをそれぞれ$a,b,c,d$、上図のように$a>b,c>d$であるとします。 ...

Read More

平方根の計算 分母の有理化

次の計算をせよ。 $$\frac{1}{\sqrt{5}-\sqrt{3}}-\frac{1}{\sqrt{3}-\sqrt{2}}+\frac{1}{\sqrt{2}-1}$$ [類・02　明海大] ...

Read More

平方根の計算 足し算・引き算

次の計算をせよ。 $$2\sqrt{12}-4\sqrt{45}+\sqrt{108}+3\sqrt{125}$$ [類・06　四国大] ...

Read More

平行四辺形の中の三角形の面積は？（1つの共通の内角をもつ平行四辺形と三角形の面積）

　「平行四辺形$\text{ABCD}$の辺$\text{CD}$を$\text{CE}:\text{ED}=1:3$に内分するような点$\text{E}$、辺$\text{DA}$上に$\text{DA}:\text{DF}=3:2$となるような点$\text{F}$がある。このとき平行四辺形$\text{ABCD}$と$△\text{DEF}$の面積の比を求めよ。」 このような問題はどのように解けばよいでしょうか？ ...

Read More

共通の内角を持つ三角形の面積を求める

「面積が$10$の$△\text{ABC}$の辺$\text{AC, BC}$上にそれぞれ $$\text{AC}:\text{PC}=3:2, \text{BC}:\text{QC}=5:3$$ となるような点$\text{P, Q}$があるとき$△\text{PQC}$の面積を求めよ。」 ...

Read More

√(-5)^2の答えはなぜ-5じゃなくて5なのか？

　$\sqrt{(-5)^2}$（ルート括弧マイナス5の2乗）の答えは$-5$ではなく$5$になります。ルートと2乗が打ち消し合ったら$-5$じゃん！と考えてしまうかもしれませんが、ちゃんと計算してみると納得し...

Read More

整式の割り算と余りの例題

　整式の割り算の問題を作ってみました。「$8x^3+x^2+6x+2$を$P_{(x)}$で割ったところ、商が$8x+1$、余りが$ax+b$となった。$a+b=17$であるとき、$P_{(x)},a,b$を求めよ。」という問題をどのように解けばよいかを考えていこうと思い...

Read More

sin36°がどんな数になるかを求めてみよう

　$36°$は$180°$の5分の1なので、「$θ$の5倍角までの$\sin,\cos,\tan$を求めてみよう」で求めた5倍角の式を利用して、$\sin36°\ (＝\sin\dfrac{\pi}{5})$がどんな数になるのかを計算してみようと思います。 ...

Read More

θの5倍角までのsin、cos、tanを求めてみよう

　別の記事で5倍角に関係する角度に触れたので、5倍角の式を求めてみようと思います。 省略している部分もありますが、計算過程も載せておきます。 ...

Read More

円周率は無理数なのに（円周）/（直径）と分数の形で定義されていることが矛盾していないことを正多角形で予測する

　円周率$\pi$は無理数である。というのを習った、あるいは聞いた覚えがあると思います。 ...

Read More

円に内接・外接する正方形の周の長さを計算してみる

　円に内接・外接する正方形の周の長さはどのくらいになるのでしょうか？計算してみました。円周と正方形の周の長さの関係から円周率の値がどのくらい絞り込めるのかも調べてみました。 ...

Read More

円に内接・外接する正三角形の周の長さを計算してみる

　半径$1$の円に内接・外接する正三角形の周の長さはいくらになるのかを計算してみます。 円周と正三角形の周の長さの関係から円周率の値がどのくらい絞り込めるのかも調べてみます。 ...

Read More

円に内接・外接する正多角形の周の長さを求める公式を作ってみよう

　円に内接・外接する正多角形の周の長さを、円の半径と正多角形の頂点の数から求めることができる式を求めてみようと思います。 ...

Read More

三角形の内心が角の二等分線の交点で求められるのはナゼ？

　三角形の内心とは、三角形に内接する円の中心のことで、3つの辺までの距離が等しいという性質があります。しかし作図する場合、三角形の内角の二等分線の交点によって求められます。 なぜ、3辺との距離が等しいという性質を利用せずに角の二等分線で作図するのでしょうか？ ...

Read More

三角形の外心が3辺の垂直二等分線の交点で求められるのはナゼ？

　三角形の外心は、外接円の中心のことで3つの頂点からの距離が等しいという性質があります。しかし、作図の場合は3辺の垂直二等分線の交点として求められます。 なぜ、頂点からの距離が等しいという性質がありながら垂直二等分線で作図するのでしょうか？ ...

Read More