摂氏温度は
華氏温度は【セ氏】(中略)一気圧における水の氷点を零度、沸点を一〇〇度として、その間を一〇〇等分したもの。
【華氏】(中略)一気圧における水の凝固点を三二度、沸点を二一二度として、その間を一八〇等分したもの。
引用:旺文社 国語辞典 第十版
とあります。(氷点=凝固点)
このことから、摂氏温度を華氏温度に変換、また華氏温度を摂氏温度に変換するにはどのような計算を行えばよいのでしょうか?
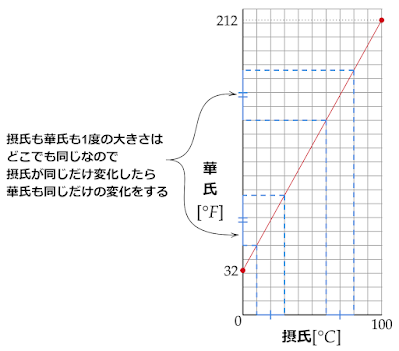
上の説明より摂氏温度の$0$度と華氏温度の$32$度、摂氏温度の$100$度と華氏温度の$212$度は水の同じ状態を指しているため、それぞれの2つの温度は対応しています。
このことから、摂氏温度と華氏温度の関係を1次関数で表すことができます。
摂氏温度を$x$度、華氏温度を$y$度とすると、この1次関数のグラフは$(0,32),(100,212)$を通るから
\begin{align*}y&=\frac{212-32}{100-0}(x-0)+32\\[0.5em]&=\frac{180}{100}x+32\\[0.5em]&=\frac{9}{5}x+32\end{align*}
となるので、摂氏温度から華氏温度に変換するためには摂氏温度の数値を$\dfrac{9}{5}$倍して$32$を加えます。
逆に華氏温度から摂氏温度を求めるには上の1次関数の逆関数を求めれば良いので
\begin{align*}x&=\frac{9}{5}y+32\\[0.5em]5x&=9y+5\cdot32\\[0.5em]9y&=5x-5\cdot32\\[0.5em]&=5(x-32)\\[0.5em]y&=\frac{5}{9}(x-32)\end{align*}
より、華氏温度の数値から$32$を引き$\dfrac{5}{9}$倍します。
Share: