2次方程式の2解が○○である条件

「2次方程式$-x^2+2kx+k^2-1=0$が次の条件を満たす$k$を求めよ。

(1)2解ともに正

(2)2解ともに$-1$以下

(3)2解の符号が異なる」

このような問題はどのように解けばよいでしょうか？

(1)2解ともに正

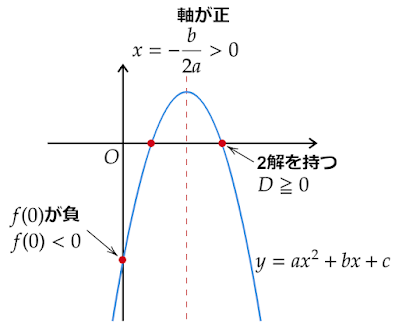
　2次方程式が2解ともに正になる条件はグラフを使って考えます。

2次方程式$ax^2+bx+c=0\ (a<0)$について、$f(x)=ax^2+bx+c$として$y=f(x)$のグラフがx軸との共有点がx軸の正の部分に存在するためには

上図のように

• 2解を持つ（1つ以上の共有点を持つ）：$D\geqq0$
• 軸がx軸の正の部分にある：$-\dfrac{b}{2a}>0$
• $f(0)$が負：$f(0)<0$

の3条件を満たしている必要があります。

このことから、

2解を持つ（1つ以上の共有点を持つ）

\begin{align*}D&=(2k)^2-4\cdot(-1)\cdot(k^2-1)\\ \\ &=4k^2+4k^2-4\\ \\ &=8k^2-4\geqq0\\ \\ &2k^2-1\geqq0\\ \\ &(\sqrt{2}k+1)(\sqrt{2}k-1)\geqq0\\ \\ &k\leqq-\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}\leqq k&\cdots(a)\end{align*}
であるから必ず2解を持ちます。

軸がx軸の正の部分にある

\begin{align*}-\frac{b}{2a}&=-\frac{2k}{2\cdot(-1)}\\ \\ &=k>0&\cdots(b)\end{align*}

$f(0)$が負

\begin{align*}f(0)=k^2-1&<0\\ \\ (k+1)(k-1)&<0\\ \\ -1<&k<1&\cdots(c)\end{align*}

　したがって、(a)、(b)、(c)より2次方程式$-x^2+2kx+k^2-1=0$が2解とも正である条件は$\dfrac{\sqrt{2}}{2}\leqq k<1$となります。

(2)2解とも$-1$以下

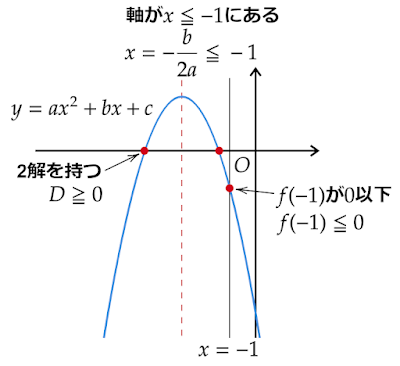
　(1)と同様に2次方程式$ax^2+bx+c=0\ (a<0)$について、$f(x)=ax^2+bx+c$として$y=f(x)$のグラフとx軸との共有点が$x=-1$以下に存在するためには

上図のように

• 2解を持つ（1つ以上の共有点を持つ）：$D\geqq0$
• 軸が$x\leqq-1$の範囲にある：$-\dfrac{b}{2a}\leqq-1$
• $f(-1)$が$0$以下：$f(-1)\leqq0$

の3条件を満たしている必要があります。

このことから、

2解を持つ（1つ以上の共有点を持つ）

(a)より

\[k\leqq-\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}\leqq k\]

軸が$x\leqq-1$の範囲にある

\[-\frac{b}{2a}=k\leqq-1\qquad\cdots(d)\]

$f(-1)$が$0$以下

\begin{align*}f(-1)&=(-1)^2+2k\cdot(-1)+k^2-1\\ \\ &=k^2-2k\leqq0\\ \\ &k(k-2)\leqq0\\ \\ &0\leqq k\leqq2&\cdots(e)\end{align*}

　したがって、(a)、(d)、(e)より2次方程式$-x^2+2kx+k^2-1=0$が2解とも$-1$以下である条件は存在しないとなります。

(3)2解の符号が異なる

　2次方程式$ax^2+bx+c=0\ (a<0)$について、$f(x)=ax^2+bx+c$として$y=f(x)$のグラフとx軸との2つの共有点のx座標の符号が異なるためには

上図のように$f(0)$が正である必要があります。

$a<0$のとき、2次関数のグラフは上に凸なのでyが常に負であるならばx軸と共有点を持つことはなく、逆にyが正になる部分があれば必ずx軸と異なる2つの共有点を持ちます。
また、yが正になる部分のxの範囲に$x=0$が含まれていれば共有点はx軸の負の部分と正の部分に1つづつ存在する、すなわちそれぞれの共有点のx座標の符号が異なることになります。

このことから、

\begin{align*}f(0)=k^2-1&<0\\ \\ (k+1)(k-1)&>0\\ \\ k<-1,&1<k\end{align*}

となります。

関連：2次方程式が2解を持つ条件

関連：2次方程式の解の公式と判別式