ありえない図形 なぜ？

　上図の（ア）～（ウ）は作図不可能な図形です。
なぜ作図不可能であることがわかるのでしょうか？

（ア）

　三角形の3辺の長さの性質、「2辺の長さの和は他の1辺の長さより大きい」を利用します。

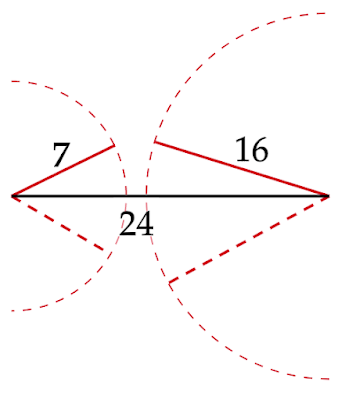
（ア）の三角形の3辺の長さはそれぞれ$7,16,24$なので

$$24>7+16=23$$

となり、2辺の長さの和より長い辺が存在するため、この性質は成り立っていません。
したがって、この三角形は作図不可能です。

　実際にこれら3つの長さの線分で三角形をつくろうとすると上図のように3つ目の頂点ができないことがわかります。

（イ）

　この四角形は1組の対辺が平行で、そのうちの1辺の両端の角が等しいので等脚台形であることがわかります。

　等脚台形の脚をそれぞれ延長して三角形をつくります。
すると底角が$60°$の二等辺三角形、すなわち正三角形になります。また、この正三角形の1辺の長さは等脚台形の下底より$8$です。

ここで等脚台形の上底に着目すると、これは正三角形の1辺に平行かつ1辺の半分の長さ$4$であることから、中点連結定理の逆より上底は正三角形においては2辺の中点同士を結ぶ線分であることがわかります。

関連：中点連結定理の逆は成り立つ？

　このことから等脚台形の脚の長さは正三角形の1辺の長さ$8$の半分、すなわち$4$となるはずなので、脚の長さが$5$である（イ）の等脚台形は作図不可能であることがわかります。

（ウ）

　この四角形は2組の対辺がそれぞれ等しいので平行四辺形であることがわかります。

ここでもう1つ平行四辺形の性質として「1つの辺の両端の角の和は$180°$である」というものがあります。

これは平行四辺形の内角の1つと内角がある辺の他端の外角は平行線の錯角であるため等しいことと、外角は$180°$と内角の差であることから確かめることができます。

しかし、（ウ）の平行四辺形は1つの辺の両端の角の和は

$$58°+112°=170°$$

であるため作図不可能であることがわかります。