通過算の問題 トンネルと列車の長さは？

「長さ$62$mの列車Aは秒速$24$mで走りトンネルを通過しきるのに$13$秒かかる。列車Bは同じトンネルを通過しきるのに$9$秒かかる。このとき列車Aと列車Bの速度の比は$3:4$であった。
トンネルと列車Bの長さはそれぞれ何mかを求めよ。」

このような問題はどのように解けばよいでしょうか？

　この問題を解くときに重要なのは列車がトンネルを通過しきるために走らなければならない距離、速度を利用した距離の求め方、そして比の計算です。

列車が走る距離

　列車がトンネルを通過し切るために走らなければならない距離について考えます。

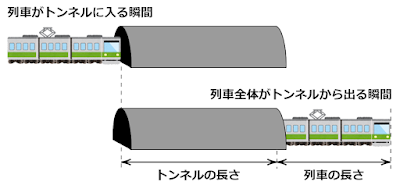
この距離は列車の先頭がトンネルに入り、列車の最後尾がトンネルから出るまでの間に列車が走った距離です。

したがって、列車が走る距離はトンネルの長さと列車の長さの和となります。

速度を使って距離を求める

　速度を使って時間を求める方法は$(距離)=(速度)×(時間)$です。

み・は・じの図からも確認できます。

比の計算

　$A:B=a:b$という比例式ができたとき、外側の数同士と内側の数同士を掛け合わせた

$$Ab=aB$$

が成り立ちます。

列車Aに着目

　トンネルの長さを$x$mとおき、列車Aに着目します。
　列車Aがトンネルを通過しきるのに走らなければならない距離は列車Aの長さ$62$mとトンネルの長さ$x$mの和なので、$(62+x)$mです。この距離を秒速$24$m、$13$秒で走るので、$(距離)=(速度)×(時間)$より
$$62+x=24\cdot13$$
という方程式ができます。

これを解くと

$$\begin{align*}62+x&=312\\ \\ x&=312-62\\ \\ &=250\end{align*}$$

よって、トンネルの長さは$250$mであるとわかります。

列車Bに着目

　次に列車Bに着目します。列車Bの長さは$y$m、速度は秒速$v$mとおきます。
　列車Aと列車Bの速度はそれぞれ秒速$24$mと秒速$v$mで、この速度の比が$3:4$なので
$$24:v=3:4$$
という関係があります。この式から比例式の計算を利用して$v$を求めると
$$\begin{align*}3v&=24\cdot4\\ \\ &=96\\ \\ v&=32\end{align*}$$
となるので、列車Bの速度は秒速$32$mであるとわかります。

　列車Bがトンネルを通過しきるのに走らなければならない距離は列車Bの長さ$y$mとトンネルの長さ$500$mの和なので、$(y+500)$mです。この距離を秒速$32$m、$9$秒で走るので、$(距離)=(速度)×(時間)$より

$$y+250=32\cdot9$$

これを解くと

$$\begin{align*}y+250&=288\\ \\ y&=288-250\\ \\ &=38\end{align*}$$

よって、列車Bの長さは$38$mであるとわかります。

　以上から、答えはトンネルの長さ$250$m、列車Bの長さ$38$mとなります。

関連：旅人算の問題　追いつくまでにかかる時間と距離は？

画像：いらすとや（https://www.irasutoya.com/）（電車）