(1)異なる2解を持つ
(2)2解を持つ
(3)2解ともに正」
解を持つ条件を調べるためには判別式を利用します。
2次方程式$ax^2+bx+c=0$の判別式$D$は
\[D=b^2-4ac\]
なので、問題の2次方程式の判別式は
\[D=k^2-4(k+3)=k^2-4k-12\]
となります。
(1)異なる2解を持つ
2次方程式が異なる2解を持つ条件は判別式の値が正となることなので、
\begin{align*}D=k^2-4k-12&>0\\ \\ (k+2)(k-6)&>0\\ \\ k<-2,&6<k\end{align*}
となります。
(2)2解を持つ
(1)と似ていますがこちらは重解も含みます。
\begin{align*}D=k^2-4k-12&\geqq0\\ \\ (k+2)(k-6)&\geqq0\\ \\ k\leqq-2,&6\leqq k\end{align*}
となります。
なぜ重解も含むのかを考えてみます。
2次方程式を因数分解して$(x-A)(x-B)=0$となったとき、$(x-A)(x-B)$が$0$になる条件は$x=A$または$x=B$の2通りになるため解が2つになります。
重解のときの2次方程式の形は$(x-A)^2=0$ですが、これは書き換えると$(x-A)(x-A)=0$であるから、同様に考えれば$x=A$または$x=A$となり、両者は同じであるものの2通りに分けることができます。
このことから重解であっても2通りの解が出てくる式の形であることは変わらないので、重解も2解を持つものに含まれます。
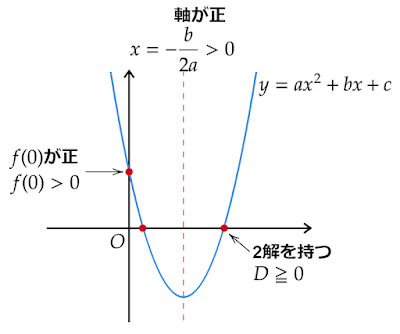
(3)2解ともに正
2次方程式の解が2つとも正になる条件はグラフを利用して考えます。
2次方程式$ax^2+bx+c=0\ (a>0)$について、$f(x)=ax^2+bx+c$として$y=f(x)$のグラフを考えると2次方程式の解はx軸との共有点のことなので、
- 2解を持つ(1つ以上の共有点を持つ):$D\geqq 0$
- 軸がx軸の正の部分にある:$-\dfrac{b}{2a}>0$
- $f(0)$が正:$f(0)>0$
の3条件を満たしている必要があります。
したがって、問題の場合は
2解を持つ
(2)より
\[k\leqq-2,6\leqq k\qquad\cdots(a)\]
軸がx軸の正の部分にある
\begin{align*}-\frac{b}{2a}=-\frac{k}{2}&>0\\ \\ k&<0&\cdots(b)\end{align*}
$f(0)$が正
\begin{align*}f(0)=0^2+k\cdot0+k+3\\ \\ =k+3&>0\\ \\ k&>-3&\cdots(c)\end{align*}
となるため、(a)、(b)、(c)より
となります。
Share: