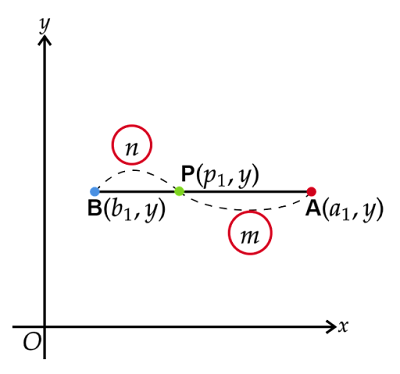
1. 線分がx軸に平行な場合
線分がy軸に平行な場合、3点のy座標は等しくなります。すなわち、の場合です。ここではy座標をとおきます。
このとき線分の長さは線分の両端の2点それぞれのy座標の差分の絶対値で求められるのでとなります。
このとき線分の長さは線分の両端の2点それぞれのy座標の差分の絶対値で求められるのでとなります。
すると、線分の長さは
線分の長さは
と表すことができます。
のとき
のとき、点の位置関係は上図と同様であり、線分の長さはと表されます。
点は点からx軸方向に線分の長さの分だけ平行移動した先にあるため、点のx座標は
すなわち、点の座標は
と表すことができます。
のとき
以上より、点のx座標の大小関係がどのようであってもx軸に平行な線分をに内分する点の座標は
となることがわかります。
2. 線分がy軸に平行な場合
線分の長さは
線分の長さは
と表すことができます。
のとき
のとき、点の位置関係は上図と同様であり、線分の長さはと表されます。
点は点からy軸方向に線分の長さの分だけ平行移動した先にあるため、点のy座標は
すなわち、点の座標は
と表すことができます。
のとき
点は点からy軸方向に線分の長さの分だけ平行移動した先にあるため、点のy座標は
すなわち、点の座標は
と表すことができます。
以上より、点のy座標の大小関係がどのようであってもy軸に平行な線分をに内分する点の座標は
となることがわかります。
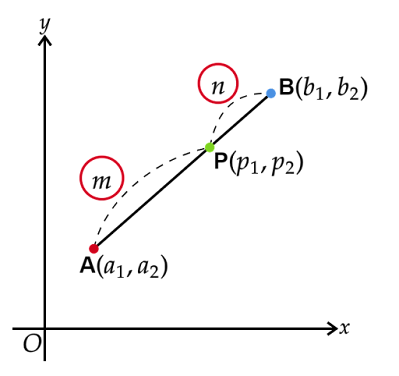
3. 線分がx軸にもy軸にも平行でない場合
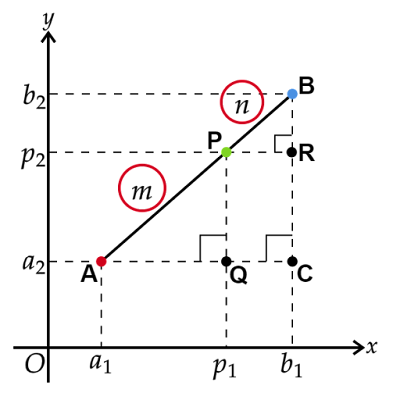
点を通るx軸に平行な直線と点を通るy軸に平行な直線を引き、その交点をとします。点は点と等しいy座標、点と等しいx座標をもちます。
また、点を通るy軸に平行な直線ととの交点を、点を通るx軸に平行な直線ととの交点をとします。点は点と等しいx座標、点は点と等しいy座標をもちます。
また、点を通るy軸に平行な直線ととの交点を、点を通るx軸に平行な直線ととの交点をとします。点は点と等しいx座標、点は点と等しいy座標をもちます。
ここでとに着目すると
- より同位角は等しいので
- x軸とy軸は垂直で、それぞれに平行な直線同士も垂直となるから
これはとの大小関係に関わらず成り立ちます。
が成り立つということは点は線分をに内分する点、点は線分をに内分する点であるということです。
すると、点のx座標と点のy座標を求めることができれば点の座標がわかります。
が成り立つということは点は線分をに内分する点、点は線分をに内分する点であるということです。
すると、点のx座標と点のy座標を求めることができれば点の座標がわかります。
線分はx軸に平行な線分でその長さはです。
したがって、より点のx座標は
したがって、より点のx座標は
と求められます。
線分はy軸に平行な線分でその長さはです。
したがって、より点のy座標は
したがって、より点のy座標は
と求められます。
以上より点の座標は
と表されることがわかります。
ここでのy座標にを代入すると
すなわちが成り立って点の座標がとなり、の場合の点の座標と一致します。
また、のx座標にを代入すると
すなわちが成り立って点の座標がとなり、の場合の点の座標と一致します。
以上より線分がどのような位置にあってもに内分する点の座標は
と表せることがわかります。
さらにのとき点の座標は
となり、中点の座標と一致します。
Share:

.png)
.png)
.png)
.png)
.png)

.png)




.png)



