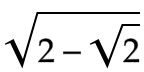上の二重根号のついた数（以下、与式）の取りうる値の範囲を計算してみます。
\begin{align*}\sqrt{2}&=1.41421356\ldots≒1.41\\ \sqrt{3}&=1.7320508\ldots≒1.73\\ \sqrt{5}&=2.2360679\ldots≒2.23\end{align*}
計算に使用する無理数は次の3つで$\sqrt{2}$を$1.41$、$\sqrt{3}$を$1.73$、$\sqrt{5}$を$2.23$とみなします。
\begin{align*}2-\sqrt{2}&=2-1.14=0.59\\ \sqrt{2-\sqrt{2}}&=\sqrt{0.59}\end{align*}
根号の中の$2-\sqrt{2}$は小数にすると$0.59$となります。したがって、与式は$\sqrt{0.59}$とも表すことができます。
しかし、$\sqrt{0.59}$は手計算で具体的にどんな値であるかを表すことが困難です。なので$\sqrt{0.59}$の値を直接求めるのではなく、$\sqrt{0.59}$に近く、$\sqrt{2}$、$\sqrt{3}$、$\sqrt{5}$を使って表すことができる数で取りうる値の範囲で表すことにします。
$\sqrt{0.59}$より大きい数で上記条件を満たすのは$\sqrt{0.60}$です。
\[0.60=\frac{2^2×3×5}{10^2}\]
$0.60$は上のように分解できるため、$\sqrt{0.60}$には$\sqrt{3}$と$\sqrt{5}$が含まれています。
これを計算すると$\sqrt{0.60}$はおよそ$0.77$となります。
$\sqrt{0.59}$より小さい数だと$\sqrt{0.54}$が該当します。
\[0.54=\frac{2×3^3}{10^2}\]
$0.54$は上のように分解できるため、$\sqrt{0.54}$には$\sqrt{2}$と$\sqrt{3}$が含まれています。
これを計算すると$\sqrt{0.54}$はおよそ$0.73$となります。
このことから、$\sqrt{0.59}$は$0.73$より大きく$0.77$より小さいことがわかります。
\begin{align*}\sqrt{0.54}<\sqrt{0.59}&<\sqrt{0.60}\\ 0.73<\sqrt{0.59}&<0.77\end{align}
よって、$\sqrt{0.59}$は与式を変換したものなので、手計算で調べた与式の取りうる値の範囲は
\begin{equation}0.73<\sqrt{2-\sqrt{2}}<0.77\end{equation}
であることが示せました。
余談
\[2\pi :8\sqrt{2-\sqrt{2}}=\pi:3.06\]
となります。円周より内接する正八角形の周の長さのほうが短いので$\pi>3.06$となるのですが、$3.06$というのは電卓を使って求めた値です。
なので、今回手計算で求めた値を使うとどのように違いがあるのかを見てみます。
まず、(1)の各辺を4倍します。
\[2.92<4\sqrt{2-\sqrt{2}}<3.08\]
すると、手計算の場合は$3.06$ではなく、$2.92$より大きく$3.08$より小さいという曖昧なものになります。
すると、手計算の場合は$3.06$ではなく、$2.92$より大きく$3.08$より小さいという曖昧なものになります。
 |
| 図1 |
これを数直線上で表してみると、上の図1のようになります。
赤い方が円周と円に内接する正八角形の周の長さの関係式、青い方が式1を表したものになります。
赤の範囲は与式の4倍は$\pi$より大きいという関係式なので、与式の4倍の値に関する青の範囲をすっぽり覆うように置かなくてはなりません。
また、$\pi$は本来およそ$3.14$という値がありますが、この記事では$\pi$の値は未定であるとして赤の範囲を描いています。
図1より、円周率の値を手計算で求めたとするのであれば、$\pi>3.06$ではなく$\pi>2.92$と書くことになります。
なので、東大入試で出たという円周率が3.05より大きいことの証明を円に内接する正八角形から導こうとするのは電卓のない状況では無理ということになりますね。
Share:
