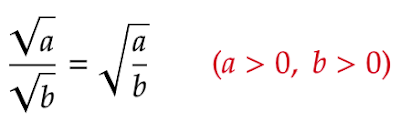平方根の計算方法を習うと出てくる式の1つに以下のものがあります。
着目してほしいのは赤字の部分。$a$と$b$がともに正の数でないと成立しないという条件がついています。それでは、$a$か$b$が負の数である場合を考えたときはどうなるのでしょうか?
その前に虚数の定義について。虚数とは負の数の平方根のことです。代表的なものは-1の平方根$\mathbf{i}$です。
\begin{align*}\sqrt{-1}&=i\\[1em]i× i&=-1\end{align*}
\begin{align*}\sqrt{-3}&=\sqrt{3×(-1)}\\[0.5em]&=\sqrt{3}×\sqrt{-1}\\[0.5em]&=\sqrt{3}i\end{align*}
虚数が含まれる計算は例えば上のように行います。これを踏まえて次に進みます。
まず一番上の平方根の計算法則の$a$と$b$にそれぞれ$-2$と$3$が与えられた場合、下のようになります。
(1)$a=-2, b=3$のとき
\begin{align*}\frac{\sqrt{-2}}{\sqrt{3}}&=\frac{\sqrt{2}i}{\sqrt{3}}\\[0.5em]&=\frac{\sqrt{2}}{\sqrt{3}}i\\[0.5em]&=\sqrt{\frac{2}{3}}i\end{align*}
$(1)$の場合、$i$と分数を切り分けることで、分数に対し平方根の計算法則を適用して計算を行うことができます。
次に$a$と$b$の正負を逆にします。
(2)$a=2, b=-3$のとき
\begin{align*}\frac{\sqrt{2}}{\sqrt{-3}}&=\frac{\sqrt{2}}{\sqrt{3}i}\\[0.5em]&=\frac{\sqrt{2}}{\sqrt{3}i}×\frac{i}{i}\\[0.5em]&=\frac{\sqrt{2}i}{-\sqrt{3}}[0.5em]&=-\frac{\sqrt{2}}{\sqrt{3}}i\\[0.5em]&=-\sqrt{\frac{2}{3}}i\end{align*}
$(2)$の場合、分母に$i$が出てきますが、そのままでは分数と$i$を切り分けることができないので、$\dfrac{i}{i}(=1)$を掛けます。
すると分母がマイナスに、分子に$i$が移るので平方根の計算法則を適用することができます。
分母と分子のどちらが虚数かで計算結果の正負が変わってしまいました。
ここで、虚数では正負が逆転するのに分母か分子のどちらかにマイナスがあっても結果が変わらないのはなんでだっけ?と思うかもしれません。
その結果、マイナスが分母、分子のどちらについているかにかかわらず、すべてマイナスが分子だけに付いている分数に変形できるので結果が変わりません。
\begin{align*}\frac{2}{-3}&=\frac{2}{-3}×\frac{-1}{-1}\\[0.5em]&=\frac{-2}{3}\\[0.5em]&=-\frac{2}{3}\end{align*}
マイナスを含む分数においては、上で$\dfrac{i}{i}(=1)$を掛けたように$\dfrac{-1}{-1}(=1)$を掛けることによって変形を行います。その結果、マイナスが分母、分子のどちらについているかにかかわらず、すべてマイナスが分子だけに付いている分数に変形できるので結果が変わりません。
Share: