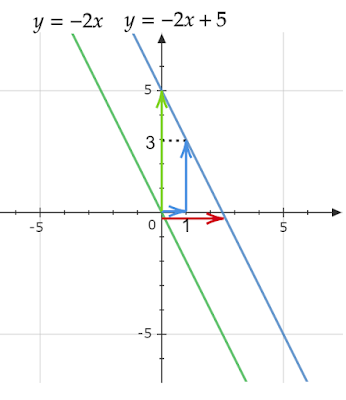
例えば、$y=-2x$を$y=-2x+5$に平行移動するとき、いくつかの方法があります。上のグラフの$y=-2x$上の原点$(0, 0)$を、$y=-2x+5$上の点へ平行移動する場合、①原点$(0, 0)$から$(2.5, 0)$へx軸方向に平行移動(赤矢印)
②原点$(0, 0)$から$(0, 5)$へy軸方向に平行移動(緑矢印)
③原点$(0, 0)$から$(1, 3)$へx軸方向とy軸方向に平行移動(青矢印)のような方法があります。原点と移動先の点にのみ着目していますが、直線上の点は同様に移動させれば、すべて平行移動後の直線上の点となります。では、①~③の各方法を軸方向への移動量がわかるように$y=-2x+5$という方程式を変形することはできるでしょうか?式を変形する
その前に直線の方程式は、$ax+by+c=0$ という形で表されます。$x,y,$定数$c$をすべて左辺に移した形を一般形と呼びます。上記の$y=-2x$と$y=-2x+5$はそれぞれ以下のようになります。\begin{align*}y=-2x\quad&\Rightarrow\quad2x+y=0\\ y=-2x+5\quad&\Rightarrow\quad2x+y-5=0\end{align*}以降直線の方程式は、この一般形で表記します。①の方法
①の方法はx軸方向に2.5 だけ平行移動しているので、\begin{align*}2x+y-5&=(2x-5)+y\\ &=2(x-\frac{5}{2})+y=0\end{align*}のように書くと括弧で囲われた部分がx軸方向に2.5(=$\frac{5}{2}$)だけ移動させていることを表していることがわかります。また、括弧の部分をXとおけば$2X+y=0$となり、元の直線$2x+y=0$を平行移動したものであるということがわかります。②の方法
この方法はy軸方向に5だけ平行移動しているので、\[2x+y-5=2x+(y-5)=0\]
と書けます。括弧の部分をYとおけば$2x+Y=0$となり、上と同じく元の直線$2x+y=0$を平行移動したものであることがわかります。③の方法
この方法はx軸方向に1、y軸方向に3だけ平行移動しているので、\begin{align*}2x+y-5&=2x+y-(2+3)\\ &=(2x-2)+(y-3)\\ &=2(x-1)+(y-3)=0\end{align*}と書けます。$x-1=X, y-3=Y$とおけば、$2X+Y=0$となり、$2x+y=0$を平行移動したものであることがわかります。
これらのことから、元の直線の方程式のxとyにx軸、y軸方向への移動量を反映させることで平行移動後の直線の方程式を求めることができることがわかります。
この記事ではこの方法を方法Aとします。
ここで、直線の平行移動には公式があり、$(p, q)$を通る$ax+by+c=0$に平行な直線の方程式は、$a(x-p)+b(y-b)=0$で表されます。これをもちいると、$a=2, b=1$、③の方法の移動先の座標から$p=1, q=3$なので\begin{align*}3(x-6)-(y-3)&=0\\ 3x-y-15&=0\end{align*}と、求めることができます。公式を使う方法をこの記事では方法Bとします。一見、方法Bは一般形の定数$c$に関係なく直線の方程式を導いているように見えます。
それなのになぜ方法Aと方法Bで同じ結果が出るのかを考えます。なぜ同じ結果になるのか?
なぜ同じ結果になるのかを、方法Aのみを使い$ax+by=0$から$ax+by+c=0$に平行移動し、さらに方法Bの$ax+by+c=0$に平行で$(p,q)$を通る直線の方程式を導くことで最終的に方法Bと同じ式を得ることを確認します。
原点を通る直線の方程式$ax+by=0$を平行移動して$ax+by+c=0$にします。このとき、$ax+by=0$上の原点$(0, 0)$が$ax+by+c=0$上の点$(m, n)$に移動するとします。
移動量はx軸方向にm、y軸方向にnとなるので、\begin{align*}a(x-m)+b(y-n)&=ax-am+by-bn\\ &=ax+by-am-bn=0\end{align*}となります。これは$ax+by+c=0$と同じ直線を表しているので、$c=-am-bn$であることがわかります。次に、この直線$ax+by+c=0$に平行で点$(p, q)$を通る直線を考えます。
$ax+by+c=0$上の点$(m, n)$が$(p, q)$に移動するので、その移動量はx軸方向に$p-m$、y軸方向に$q-n$となります。
したがって、\begin{align*}&a\left\{x-(p-m)\right\}+b\left\{y-(q-n)\right\}+c\\ =&ax-ap+am+by-bq+bn+c\\ =&ax+by+(-ap+am-bq+bn+c)\\ =&ax+by+(-ap+am-bq+bn-am-bn)\\ =&ax+by-ap-bq=0\end{align*}となります。前述の通り$c=-am-bn$であるので、展開して出てきた$am+bn$とで定数cは打ち消され$-ap-bq$だけが定数部分として残ります。そして、\begin{align*}&ax+by-ap-bq\\ =&a(x-p)+b(y-q)=0\end{align*}と変形できることから、「$ax+by+c=0$に平行で点$(p, q)$を通る直線」を考えるときは、「原点を通る直線$ax+by=0$に平行で$(p, q)$を通る直線」に置き換えて考えることができ、置き換えた式が方法Bの直線の平行移動の公式となっていることがわかります。なので、方法Aと方法Bは同じ結果になります。
また、方法Bは定数cと関係のない原点を通る直線を元にして平行移動していることになるので、定数cについては考えなくても平行移動は可能であるということがわかります。
出典:Plmbago雑記(改変あり)